- 其它不等式的解法
- 共267题
正确答案
解析
作出可行域,直线



知识点
若点(x,y)位于曲线y=|x-1|与y=2所围成的封闭区域,则2x-y的最小值为__________。
正确答案
-4
解析
由y=|x-1|=
令2x-y=z,则y=2x-z,画直线l0:y=2x并平移到过点A(-1,2)的直线l,此时-z最大,即z最小=2×(-1)-2=-4
知识点
已知变量


正确答案
解析
略。
知识点
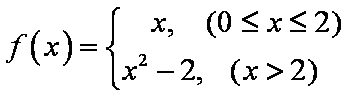
已知函数

正确答案
解析
考查分段函数的单调性。
知识点
已知函数f(x)=x(1+a|x|),设关于x的不等式f(x+a)<f(x)的解集为A.若
正确答案
解析
f(x)=x(1+a|x|)=
若不等式f(x+a)<f(x)的解集为A,且
则在区间
(1)当a=0时,显然不符合条件。
(2)
当a>0时,画出函数y=f(x)和y=f(x+a)的图象大致如图。
由图可知,当a>0时,y=f(x+a)的图象在y=f(x)图象的上边,故a>0不符合条件。
(3)
当a<0时,画出函数y=f(x)和y=f(x+a)的图象大致如图。
由图可知,若f(x+a)<f(x)的解集为A,且
只需
则有
整理,得a2-a-1<0,解得
∵a<0,∴a∈
综上,可得a的取值范围是
知识点
设




正确答案
2
解析
此不等式表示的平面区域如下图4所示:
当





知识点
设a
正确答案
解析
本题按照一般思路,则可分为一下两种情况:
(A)
(B)
因为受到经验的影响,会认为本题可能是错题或者解不出本题,其实在x>0的整个区间上,我们可以将其分成两个区间(为什么是两个?),在各自的区间内恒正或恒负,(如下答图)
我们知道:函数y1=(a-1)x-1,y2=x 2-ax-1都过定点P(0,1)。
考查函数y1=(a-1)x-1:令y=0,得M(
考查函数y2=x 2-ax-1:显然过点M(




知识点
若不等式组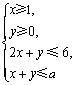
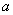
正确答案
(3,5)
解析
略
知识点
若全集为实数集


正确答案
解析
略。
知识点
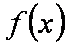
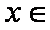
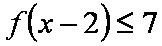
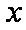
正确答案
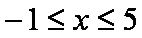
解析
画出函数y=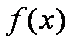
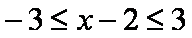
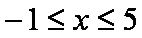
知识点
扫码查看完整答案与解析
























