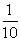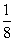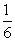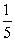- 两条直线平行与倾斜角、斜率的关系
- 共45题
1
题型:填空题
|
函数

正确答案
解析

知识点
两条直线平行与倾斜角、斜率的关系
1
题型:
单选题
|
从正六边形的6个顶点中随机选择4个顶点,则以它们作为顶点的四边形是矩形的概率等于
正确答案
D
解析
略
知识点
两条直线平行与倾斜角、斜率的关系
1
题型:简答题
|
如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C。
(1)证明:B1C⊥AB;
(2)若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱ABC﹣A1B1C1的高。
正确答案
见解析。
解析
(1)连接BC1,则O为B1C与BC1的交点,∵侧面BB1C1C为菱形,
∴BC1⊥B1C,∵AO⊥平面BB1C1C,∴AO⊥B1C,∵AO∩BC1=O,∴B1C⊥平面ABO,
∵AB⊂平面ABO,∴B1C⊥AB;
(2)作OD⊥BC,垂足为D,连接AD,作OH⊥AD,垂足为H,∵BC⊥AO,BC⊥OD,AO∩OD=O,
∴BC⊥平面AOD,∴OH⊥BC,∵OH⊥AD,BC∩AD=D,∴OH⊥平面ABC,∵∠CBB1=60°,
∴△CBB1为等边三角形,∵BC=1,∴OD=


由OH•AD=OD•OA,可得AD=


∵O为B1C的中点,∴B1到平面ABC的距离为
知识点
两条直线平行与倾斜角、斜率的关系
1
题型:简答题
|
在△ABC中,内角


(1)求证:
(2)若

正确答案
见解析。
解析
(1)由已知得:



再由正弦定理可得:
所以
(2)若

∴

∴△

知识点
两条直线平行与倾斜角、斜率的关系
1
题型:填空题
|
如图已知圆中两条弦




线上一点,且
若

正确答案
解析
设





∴
由切割定理得
∴
知识点
两条直线平行与倾斜角、斜率的关系
下一知识点 : 两条直线垂直的判定
扫码查看完整答案与解析