三角函数的图象与性质
共601题

三角函数的图象与性质
共601题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

四面体的外接球球心在上，且，在外接球面上、两点间的球面距离是

正确答案

解析

略

知识点

正弦函数的对称性

题型：简答题

简答题 · 12 分

在中，角所对的边分别为，且满足

（1）求角的大小；

（2）求的最大值，并求取得最大值时角的大小。

正确答案

见解析。

解析

（1）由正弦定理得sinCsinA=sinAcosC，

∵0＜A＜π，

∴sinA＞0，

∴sinC=cosC，又cosC≠0，

∴tanC=1，又C是三角形的内角

即∠C=…

（2）sinA﹣cos（B+C）=sinA﹣cos（π﹣A）

=sinA+cosA=2sin（A+）…

又0＜A＜，＜A+＜，

所以A+=即A=时，2sin（A+）取最大值2。

综上所述，sinA﹣cos（B+C）的最大值为2，此时A=，B=…

知识点

正弦函数的对称性

题型：简答题

简答题 · 16 分

在中，角，，所对的边分别是，，，已知，.

（1）若的面积等于，求，；

（2）若，求的面积.

正确答案

见解析。

解析

（1）由余弦定理及已知条件得，，

又因为的面积等于，所以，得，

联立方程组解得，，

（2）由题意得，即，

当时，，，，，

当时，得，由正弦定理得，

联立方程组解得，，

所以的面积，

知识点

正弦函数的对称性

题型：单选题

单选题 · 5 分

运行如图1的程序框图，则输出s的结果是

正确答案

解析

略

知识点

正弦函数的对称性

题型：单选题

单选题 · 5 分

函数f (x) =的图像相邻的两条对称轴之间的距离是

正确答案

解析

f (x) =cos+ sin

= 2(sincos+ cossin)

= 2sin

∴周期为T =

则相邻的对称轴间的距离为

知识点

正弦函数的对称性三角函数中的恒等变换应用

题型：填空题

填空题 · 4 分

若则

正确答案

解析

略

知识点

正弦函数的对称性

题型：简答题

简答题 · 12 分

已知为的内角的对边，满足，函数在区间上单调递增，在区间上单调递减。

（1）证明：；

（2）若，证明为等边三角形。

正确答案

见解析。

解析

（1）

………………………………………………………3分

………………………………………………………………………5分

所以 ………………………………………………………………………………6分

（2）由题意知：由题意知：，解得：， …………………………8分

因为, ,所以 …………………………9分

由余弦定理知： ………………………………………10分

所以因为，所以，

即：所以 ………………………………………………………11分

又，所以为等边三角形. …………………………………………………12分

知识点

正弦函数的对称性

题型：单选题

单选题 · 5 分

函数（）的图象的一条对称轴方程是（）

正确答案

解析

略

知识点

正弦函数的对称性

题型：单选题

单选题 · 5 分

函数的图象（　）

A关于对称

B关于y轴对称

C关于原点对称

D关于对称

正确答案

解析

略

知识点

函数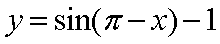的图象与图象变化正弦函数的图象正弦函数的对称性诱导公式的作用

题型：简答题

简答题 · 8 分

已知，函数

（1）求的最小正周期，并求其图象对称中心的坐标；

（2）当时，求函数f(x)的值域.

正确答案

见解析。

解析

（1）

………2分

所以的最小正周期为

令，得。

故所求对称中心的坐标为- ………4分

（2） ………6分

即的值域为　　 - ………8分

知识点

三角函数的周期性及其求法正弦函数的定义域和值域正弦函数的对称性三角函数中的恒等变换应用数量积的坐标表达式

继续学习学习下一知识点

下一知识点 : 三角恒等变换

百度题库 > 高考 > 文科数学 > 三角函数的图象与性质

扫码查看完整答案与解析