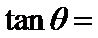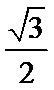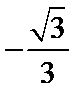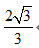- 三角恒等变换
- 共635题
7.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是
正确答案
解析
该几何体直观图如图所示:
考查方向
解题思路
由于三视图能有效的考查学生的空间想象能力,所以以三视图为载体的立体几何题基本上是高考每年必考内容,高考试题中三视图一般常与几何体的表面积与体积交汇.由三视图还原出原几何体,是解决此类问题的关键.
易错点
由三视图正确还原出原几何体
知识点
17.已知


(1)求
(2)在




与


正确答案
解析
试题分析:本题属于向量结合三角函数以及解三角形的问题,题目的难度是逐渐由易到难,(1)直接根据题意得到函数的解析式再使用辅助角公式合二为一化简之后再求单调区间;(2)利用正余弦定理来解三角形。
(1)由题意知





(2)






因为向量


由正弦定理得

考查方向
解题思路
本题考查向量结合三角函数以及解三角形的问题,解题步骤如下:(1)直接根据题意得到函数的解析式再使用辅助角公式合二为一化简之后再求单调区间;(2)利用正余弦定理来解三角形。
易错点
第一问忘记写
知识点
4.若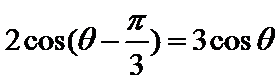
正确答案
解析
由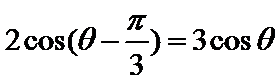
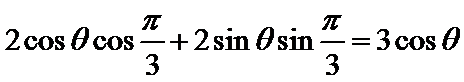
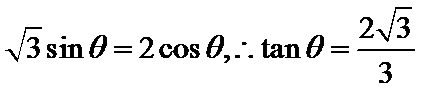
考查方向
解题思路
先根据两角差的余弦公式将题中给出的等式化简为关于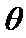
易错点
不会利用两角差的余弦公式展开题中给出的条件,对于的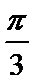
知识点
13. 已知

正确答案
解析



考查方向
解题思路
先求出
易错点
计算错误,对公式定理掌握不好
知识点
已知

16.求
17.求函数

正确答案

解析
解:由已知得
所以

又因为
所以
考查方向
解题思路
利用同角关系可以得到
易错点
容易忽略条件在
正确答案

解析
由(Ⅰ)得
由
所以 当

当

所以函数

考查方向
解题思路
利用同角关系可以得到
易错点
容易忽略条件在
6.已知

正确答案
解析

考查方向
解题思路
首先由利用诱导公式将
易错点
1、本题易在使用诱导公式时判断错误符号而导致出错。
2、本题容易因为公式记忆不清楚而出现错误。
知识点
已知向量

(1)求 tanA的值;
(2)求函数
正确答案
见解析。
解析
(1)m·n=sinA-2cosA=0,得tanA=2.
(2)
当

所以f(x)的值域是
知识点
若

正确答案
解析
略
知识点
9.将最小正周期为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若角


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析