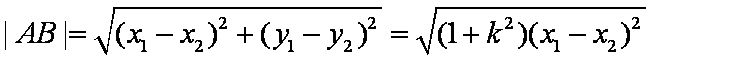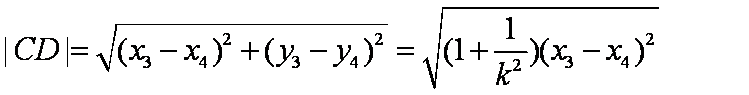- 三角函数的图象与性质
- 共601题
已知函数f(x)=2sin(x=


(1)求f(x)的最小正周期;
(2)求函数f(x)的单调递增区间。
正确答案
见解析。
解析
(1)∵f(x)=2sin(x+


=sin(2x+

=


=

∴f(x)的最小正周期T=π
(2)由(1)知f(x)=

当﹣


即kπ﹣



∴函数f(x)的单调递增区间为[kπ﹣

知识点
已知函数

(1)求函数
(2)当



正确答案
(1)

解析
解析:
(2)因为

函数的增区间为
知识点
已知函数

(1)求函数
(2)若函数




正确答案
见解析。
解析
(1)



当

函数

(2)函数





即


知识点
已知


(1)求方程
(2)求函数
正确答案
见解析
解析
(1)
由


故方程

(2)

∴函数

由
故函数

知识点
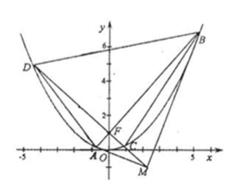
已知抛物线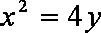
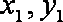
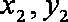
(1)求A,B两点的横坐标之积;
(2)求证:A、M、B三点的横坐标成等差数列;
(3)设直线MF交该抛物线于C,D两点,求四边形ACBD面积的最小值。
正确答案
见解析
解析
(1)由已知,得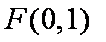
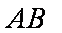
则可设直线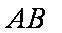
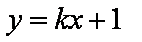
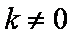
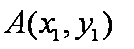
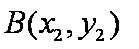
由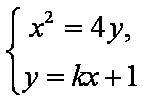
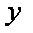
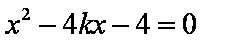
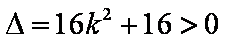
所以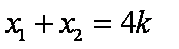
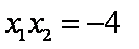
即
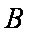
(2)由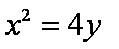
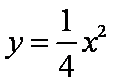
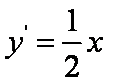
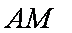
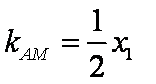
所以,直线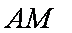
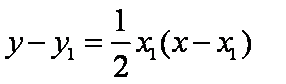
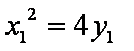
所以,直线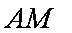
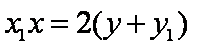
同理,直线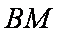
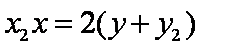
②-①并据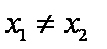
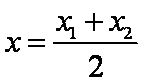
即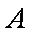
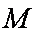
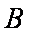
(3)由①②易得y=-1,所以点M的坐标为(2k,-1)(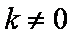
所以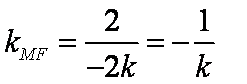
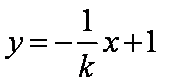
设C(x3,y3),D(x4,y4)
由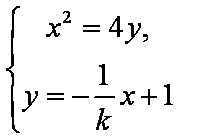
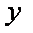
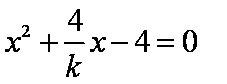
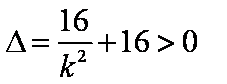
所以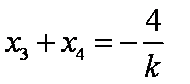
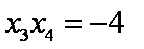
又
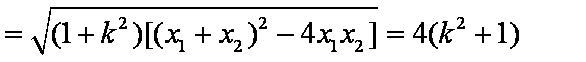
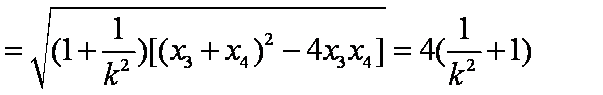
因为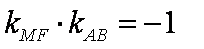
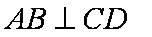
所以,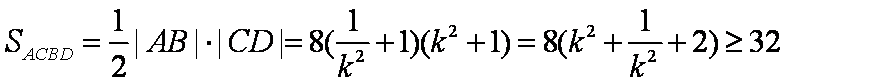
当且仅当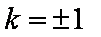
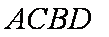
知识点
设
(1)求函数
(2)当
正确答案
见解析。
解析
(1)

所以函数的单调递增区间是
(2)

知识点
已知
(1)求
(2)当
正确答案
见解析。
解析
(1)

所以
令

故所求对称中心的坐标为
(2)

即

知识点
已知函数
(1)求函数
(2)设







正确答案
见解析
解析
(1)原式可化为: 



(2)由





又由余弦定理,得

联立①、②解得
知识点
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求
(2)将




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析