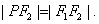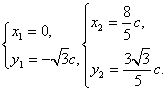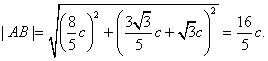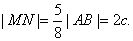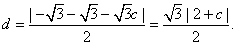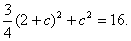- 椭圆及其性质
- 共629题
18.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
已知中心在原点的椭圆C的右焦点为

正确答案
解析
由焦点可知



知识点
已知




正确答案
解析
在双曲线




知识点
已知椭圆





(1)求椭圆
(2)当


正确答案
(1)
解析
(1)由题意得
解得
所以椭圆

(2)由

设点







所以

又因为点


所以

由
知识点
设椭圆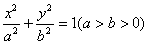
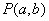
(1)求椭圆的离心率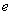
(2)设直线PF2与椭圆相交于A,B两点,若直线PF2与圆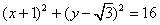
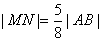
正确答案
(1) 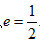
解析
(1)解:设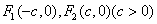
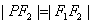
所以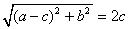
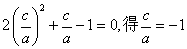
或
(2)解:由(Ⅰ)知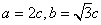
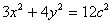
A,B两点的坐标满足方程组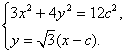
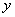
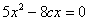
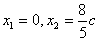
不妨设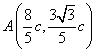
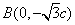
于是
圆心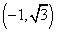
因为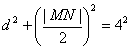
整理得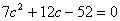
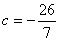
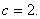
知识点
设










正确答案
解析
∵△

∴






知识点
设椭圆C:
正确答案
解析
如图所示,在Rt△PF1F2中,|F1F2|=2c,
设|PF2|=x,则|PF1|=2x,
由tan 30°=

而由椭圆定义得,|PF1|+|PF2|=2a=3x,
∴
知识点
已知椭圆



正确答案
解析
略
知识点
已知椭圆


(1)求椭圆的离心率;
(2)设A为椭圆的左顶点,O为坐标原点,若点Q在椭圆上且满足|AQ|=|AO|,求直线OQ的斜率的值。
正确答案
(1) 
解析
(1)因为点P(



于是

(2)设直线OQ的斜率为k,则其方程为y=kx,设点Q的坐标为(x0,y0)。
由条件得

由|AQ|=|AO|,A(-a,0)及y0=kx0,得(x0+a)2+k2x02=a2,整理得(1+k2)x02+2ax0=0,而x0≠0,故

由(1)知

即5k4-22k2-15=0,可得k2=5。
所以直线OQ的斜率
知识点
已知椭圆C: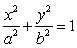
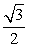
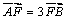
正确答案
解析
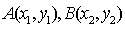
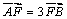
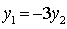
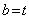
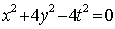
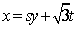
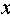
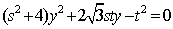
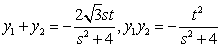
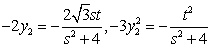
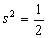
知识点
扫码查看完整答案与解析