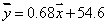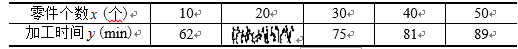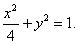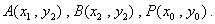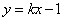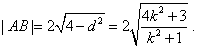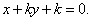椭圆及其性质_章节学习

1

题型：简答题

|

简答题 · 14 分

如图,椭圆的两个焦点分别为、,且到直线的距离等于椭圆的短轴长。

(1) 求椭圆的方程；

(2) 若圆的圆心为(),且经过、,是椭圆上的动点且在圆外,过作圆的切线,切点为,当的最大值为时,求的值。

正确答案

见解析。

解析

(1)设椭圆的方程为(),

依题意,,

所以

又,

所以,

所以椭圆的方程为.

(2) 设(其中),

圆的方程为,

因为,

所以

当即时,当时,取得最大值,

且,解得(舍去)。

当即时,当时,取最大值,

且,解得,又,所以.

综上,当时,的最大值为.

知识点

椭圆的定义及标准方程

1

题型：简答题

|

简答题 · 14 分

已知椭圆：的两个焦点分别为，，离心率为，且过点.

（1）求椭圆的标准方程；

（2），，，是椭圆上的四个不同的点，两条都不和轴垂直的直线和分别过点，，且这两条直线互相垂直，求证：为定值。

正确答案

见解析

解析

（1）解：由已知，

所以.

所以：，即.

因为椭圆过点，

得，.

所以椭圆的方程为.

（2）证明：由（1）知椭圆的焦点坐标为，.

根据题意，可设直线的方程为，

由于直线与直线互相垂直，则直线的方程为.

设，.

由方程组消得

.

则 .

所以=.

同理可得.

所以.

知识点

椭圆的定义及标准方程

1

题型：单选题

|

单选题 · 5 分

某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验，根据收集到的数据（如下表），由最小二乘法求得回归直线方程

表中有一个数据模糊不清，请你推断出该数据的值为

A68

B68.2

C68.5

D75

正确答案

A

解析

略

知识点

椭圆的定义及标准方程

1

题型：填空题

|

填空题 · 5 分

椭圆的两个焦点为，点在椭圆上,若,则。

正确答案

5

解析

略

知识点

椭圆的定义及标准方程

1

题型：简答题

|

简答题 · 13 分

已知椭圆C：的右焦点F在圆D：上，直线交椭圆于M、N两点。

（1）求椭圆C的方程；

（2）若（O为坐标原点）求m的值；

（3）若点P的坐标是（4，0），试问的面积是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由.

正确答案

见解析。

解析

知识点

椭圆的定义及标准方程

1

题型：简答题

|

简答题 · 14 分

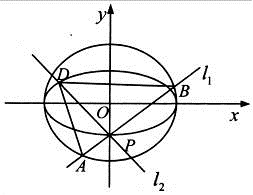
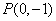
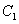
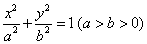
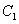
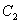
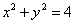
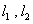
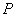
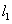
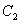
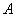
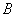
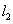
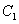
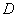
如图，点是椭圆：的一个顶点，的长轴是圆：

的直径，是过点且互相垂直的两条直线，其中交圆于、两点，

交椭圆于另一点。

(1) 求椭圆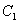的方程；

(2) 求△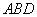面积的最大值及取得最大值时

直线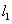的方程。

正确答案

见解析。

解析

（1）由题意得

∴椭圆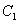的方程为

（2）设

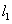
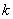
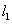
由题意知直线的斜率存在，不妨设其为，则直线的方程为

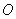
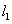
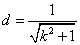
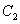
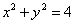
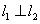
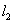
故点到直线的距离为，又圆：，

∴

又，∴直线的方程为

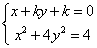
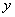
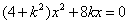
由，消去，整理得，

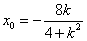
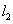
故，代入的方程得

∴

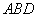
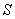
设△的面积为，则

∴

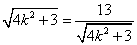
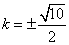
当且仅当，即时上式取等号。

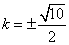
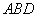
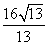
∴当时，△的面积取得最大值，

此时直线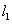的方程为

知识点

椭圆的定义及标准方程

1

题型：简答题

|

简答题 · 13 分

设椭圆的左、右焦点分别为，离心率为，左焦点到直线的距离等于长半轴长。

（1）求椭圆的方程；

（2）过右焦点作斜率为的直线与椭圆交于两点，线段的中垂线与轴相交于点，求实数的取值范围。

正确答案

（1）

（2）

解析

（1）由已知可得，

由到直线的距离为，所以，，，，，，，，，，，，3分

解得

所求椭圆方程为. ，，，，，，，，，，，，，，，，5分

（2）由（1）知, 设直线的方程为：

消去得，，，，，7分

因为过点，所以恒成立

设，

则，

中点，，，，，，，，，，，，，，，9分当时，为长轴，中点为原点，则，，，，，，，，，，，，，，10分

当时中垂线方程，

令，，，，，，，，，，11分

，，可得

综上可知实数的取值范围是，，，，，，，，，，，，，，，13分

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线中的范围、最值问题

1

题型：简答题

|

简答题 · 14 分

已知椭圆和直线L:=1, 椭圆的离心率，直线L与坐标原点的距离为。

（1）求椭圆的方程；

（2）已知定点，若直线与椭圆相交于C、D两点，试判断是否存在值，使以CD为直径的圆过定点E？若存在求出这个值，若不存在说明理由。

正确答案

见解析。

解析

（1）直线L:=1,∴=.① ，，，，，，，，，，，，，，，，，，2分

e=.② ，，，，，，，，，，，，，，，，，，4分

由①得，3

由②3得 ∴所求椭圆的方程是+y2=1. ，，，，，，，，，，，，，，，，，，6分

（2）联立得：.

Δ ，，，，，，，，，，，，8分

设，则有

，，，，，，，，，，，，，，，，，，10分

∵，且以CD为圆心的圆点过点E，

∴EC⊥ED. ，，，，，，，，，，，，，，，，，，12分

则

∴，解得=＞1,

∴当=时以CD为直径的圆过定点E. ，，，，，，，，，，，，，，，，，。14分

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线中的探索性问题

1

题型：单选题

|

单选题 · 5 分

若双曲线y2=4（m>0）的焦距为8，则它的离心率为

A

B2

C

D

正确答案

A

解析

略

知识点

椭圆的定义及标准方程

1

题型：简答题

|

简答题 · 14 分

已知圆：,若椭圆：（）的右顶点为圆的圆心，离心率为.

（1）求椭圆的方程；

（2）已知直线：，若直线与椭圆分别交于，两点，与圆分别交于，两点（其中点在线段上），且，求的值。

正确答案

（1）

（2）

解析

（1）设椭圆的焦距为，因为，，所以………………2分

所以所以椭圆：………………4分

（2）设（，），(，)

由直线与椭圆交于两点，，则

所以, 则，………………6分

所以………………8分

点(）到直线的距离………………10分

则………………11分

显然，若点也在线段上，则由对称性可知，直线就是轴，矛盾，

因为，所以………………12分

所以

解得,即………………14分

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点