空间向量与立体几何
共9778题

空间向量与立体几何
共9778题

热门试卷

X 查看更多试卷

题型：填空题

填空题

已知=（1，2，-1），=（x，y，2），且∥，那么x+y=______．

正确答案

-6

解析

解：∵=（1，2，-1），=（x，y，2），

又∵∥，

则存在λ∈R，使=λ

即（1，2，-1）=λ（x，y，2），

∴

解得λ=-

∴x=-2，y=-4

∴x+y=-6

故答案为：-6．

题型：简答题

简答题

（2015春•广安校级月考）已知点A、B、C的坐标分别为（0，1，2），（1，2，3），（1，3，1）．

（1）若，且⊥，求y的值；

（2）若D的坐标为（x，5，3），且A，B，C，D四点共面，求x的值．

正确答案

解：（1）=（1，2，-1），∵⊥，∴=3+2y-1=0，解得y=-1．

（2）=（1，2，-1），=（1，1，1），=（x，4，1），

∵A，B，C，D四点共面，

∴存在唯一一对实数m，n，使得，

∴，解得，

∴x=3．

解析

解：（1）=（1，2，-1），∵⊥，∴=3+2y-1=0，解得y=-1．

（2）=（1，2，-1），=（1，1，1），=（x，4，1），

∵A，B，C，D四点共面，

∴存在唯一一对实数m，n，使得，

∴，解得，

∴x=3．

题型：单选题

单选题

已知，则与向量共线的单位向量是（　　）

正确答案

解析

解：∵，

∴与向量共线的单位向量是

±=±（1，-1，1）=±（，-，）．

故选：D．

题型：填空题

填空题

若A（-1，0，1），B（x，y，4），C（1，4，7），且A、B、C三点在同一直线上，则实数x-y=______．

正确答案

-2

解析

解：∵A（-1，0，1），B（x，y，4），C（1，4，7），∴=（x+1，y，3），=（2，4，6）．

∵A、B、C三点在同一直线上，∴存在实数k使得．

∴，解得．

∴x-y=-2．

故答案为：-2．

题型：单选题

单选题

对于空间三个向量、、，它们一定是（　　）

A共线向量

B不共线向量

C共面向量

D不共面向量

正确答案

解析

解：由题意

由空间向量基本定理知空间三个向量、、一定共面

故选C

题型：填空题

填空题

已知=（2，4，-5），=（3，x，y），若∥，则实数x+y=______．

正确答案

解析

解：∵∥，

∴==，

解得x=6，y=-，

故x+y=6-=-．

故答案为：-．

题型：简答题

简答题

已知点A，B，C的坐标依次是（-1，0，1）（2，4，3）（5，8，5），求证：三点共线．

正确答案

解：∵向量=（2+1，4-0，3-1）=（3，4，2），

向量=（5+1，8-0，5-1）=（6，8，4）；

∴=2，

又与有公共点A，

∴A、B、C三点共线．

解析

解：∵向量=（2+1，4-0，3-1）=（3，4，2），

向量=（5+1，8-0，5-1）=（6，8，4）；

∴=2，

又与有公共点A，

∴A、B、C三点共线．

题型：填空题

填空题

（2015秋•盐城校级期末）已知，若，则mn=______．

正确答案

1或-

解析

解：∵，

∴存在实数k使得，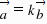

∴，解得，或．

则mn=1或-．

故答案为：1或-．

题型：单选题

单选题

下列各组向量共面的是（　　）

正确答案

解析

解：利用向量共面定理可知：如果存在实数m，n使得成立，则向量，，共面．

经过判定：对于A：=，而B，C，D不满足向量共面定理．

故选：A．

题型：填空题

填空题

已知向量=（1，2，3），=（x，4，6），若∥，则x的值为______．

正确答案

解析

解：∵向量=（1，2，3），=（x，4，6），

且∥，

∴==

∴x=2

故答案为：2．

题型：填空题

填空题

若点A（1，1，1），B（2，3，4），O（4，x，y）三点共线，则x+y=______．

正确答案

解析

解：由A（1，1，1），B（2，3，4），O（4，x，y），

可得

．

因为A（1，1，1），B（2，3，4），O（4，x，y）三点共线，

所以，解得x=5，y=7．

所以x+y=12．

故答案为12．

题型：填空题

填空题

若直线l的方向向量为=（1，0，2），平面α的法向量为=（-2，0，-4），则直线与平面的位置关系是______．

正确答案

l⊥α

解析

解：∵=-2，

∴，

因此l⊥α．

故答案为：l⊥α．

题型：单选题

单选题

下列各组向量中不平行的是（　　）

正确答案

解析

解：选项A，由已知数据可得=-2，故向量平行，故错误；

选项B，由已知数据可得=-3，故向量平行，故错误；

选项C，由已知数据可得=0，故向量平行，故错误；

选项D，由已知数据可得，不存在实数使一个向量用另一个表示，

故向量不平行，故正确；

故选D

题型：填空题

填空题

已知点A（1，2，1），B（-1，3，4），且，则P的坐标是______．

正确答案

解析

解：设P（x，y，z）．

∵，∴（x-1，y-2，z-1）=2（-1-x，3-y，4-z）=（-2-2x，6-2y，8-2z）．

∴，解得．

∴P．

故答案为：．

题型：单选题

单选题

（理科）已知直线l的一个方向向量的坐标为=（1，-1，2）且过点M（3，1，4），那么以下各点中在直线l上的是（　　）

A（3，-1，2）

B（6，-1，8）

C（3，-1，8）

D（5，-1，8）

正确答案

解析

解：若点P在直线l上，则=（λ，-λ，2λ），

∴=（3，1，4）+（λ，-λ，2λ），

经验证：只有点P取（6，-1，8）时，存在λ=2满足条件，

故选：B．

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 数学 > 空间向量与立体几何

扫码查看完整答案与解析