- 空间向量与立体几何
- 共9778题
空间直角坐标系中,A(1,2,3),B(-2,-1,6),C(3,2,1),D(4,3,0),则直线AB与CD的位置关系是( )
正确答案
解析
解:∵

∴
∴
∵点A不在直线AB上.
∴AB∥CD.
故选:B.
对于空间任意一点O和不共线的三点A、B、C,有如下关系:6



正确答案
解析
解:由已知得



而


∴四点P、A、B、C共面.
故选:B.
(2015秋•安庆校级期末)已知




正确答案
3
解析
解:∵向量

∴存在唯一一对实数m,n使得
∴

故答案为:3.
已知向量



正确答案
解析
解:向量

并且

∴
解得

当x=-1、y=-3时,

∴x,y的值为
故答案为:
四棱锥P-ABCD中,底面ABCD是平行四边形,


正确答案
解析
证明:(1)∵


∴

∴AP⊥AB,AP⊥AD,
即AP⊥AB且AP⊥AD,
又∵AB∩AD=A
∴AP⊥平面ABCD;
故选B.
O、A、B、C为空间四个点,又


正确答案
解析
解:由基底意义,


但A、B、C三种情形都有可能使


只有D才能使这三个向量不共面,
故应选D.






正确答案


又∵BM=
∴GM∥AB,又∵AB∥CD,
∴GM∥CD,
同理,GN∥DE,
故由GN、GM、MN共面可知,
向量


解析


又∵BM=
∴GM∥AB,又∵AB∥CD,
∴GM∥CD,
同理,GN∥DE,
故由GN、GM、MN共面可知,
向量


在四面体ABCD中,点G1,G2,G3,G4分别为△ABC,△ACD,△ADB,△BCD的重心,点M在线段AG4上,且AM:MG4=2:1,求证:向量


正确答案
证明:如图所示,
四面体ABCD中,点G1,G2,G3,G4分别为△ABC,△ACD,△ADB,△BCD的重心,
延长AG1交BC于点E,
∴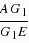

又AM:MG4=2:1,
∴

∴G1M∥EG4;
又G1M⊄平面BCD,EG4⊂平面BCD,
∴G1M∥平面BCD;
同理G1G2∥平面BCD,G1G3∥平面BCD,
且G1M∩G1G2=G1,G1M∩G1G3=G1,
∴G1M、G1G2、G1G3三线共面,
即向量


解析
证明:如图所示,
四面体ABCD中,点G1,G2,G3,G4分别为△ABC,△ACD,△ADB,△BCD的重心,
延长AG1交BC于点E,
∴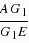

又AM:MG4=2:1,
∴

∴G1M∥EG4;
又G1M⊄平面BCD,EG4⊂平面BCD,
∴G1M∥平面BCD;
同理G1G2∥平面BCD,G1G3∥平面BCD,
且G1M∩G1G2=G1,G1M∩G1G3=G1,
∴G1M、G1G2、G1G3三线共面,
即向量


已知


正确答案
解析
解:∵

∴存在实数λ使得
∴


故答案分别为:

已知向量




正确答案
解:2
∵



∵α是第二象限角,∴

∴

故答案为:
解析
解:2
∵



∵α是第二象限角,∴

∴

故答案为:
已知A(1,2,1),B(-1,3,4),C(1,1,1),


正确答案
解析
解:∵


化为




∴


故选:D.
下列条件使M与A,B,C一定共面的是( )
正确答案
解析
解:对于D:
同理可得:A,B,C,不一定共面.
故选:D.
已知向量

正确答案
解析
解:与



故答案为:
若


正确答案
解析
解:∵


可设

则(1,-2y,9)=λ(2x,1,3),
即
解得λ=3,x=

故选:C.
对于空间中的三个向量



正确答案
解析
解:∵






故选A.
扫码查看完整答案与解析






































