- 等差数列的基本运算
- 共139题
5.设
A
B
C
D
正确答案
解析
由
考查方向
解题思路
本题解答过程中用到了的等差数列的一个基本性质即等差中项的性质,利用此性质可得
易错点
等差中项的性质的正确应用要注意下标关系
知识点
3．已知等差数列
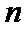
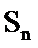
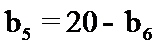
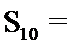
正确答案
解析
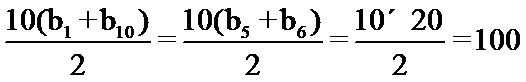
考查方向
解题思路
利用等差数列的求和公式表示出前10项的和，再利用等差数列的性质即可解出。
易错点
不会利用等差数列的性质来求解。
知识点
7.已知
A
B
C10
D12
正确答案
知识点
10.将所有正偶数按如下方式进行排列，则2 016位于
第1行：2 4
第2行：6 8 10 12
第3行：14 16 18 20 22 24
第4行：26 28 30 32 34 36 38 40
…… …… ……
正确答案
解析
因为2016是第1008个偶数，按照题意进行排列，得到一个新的等差数列，
考查方向
解题思路
1)计算2016是第几个正偶数；
2)求新的等差数列的通项公式；
3)找出2016在第几行.
易错点
本题易在运算上出现错误，也容易在项数上出现错误。
知识点
3. 设
A
B
C
D
正确答案
考查方向
本题主要考查了数列的定义、等比数列的基本量运算与公式，在近几年的各省高考题出现的频率较高，常单独命题或与等差数列给合，考查基本公式、运算和性质。
解题思路
由方程思想列出关于公差与首项的等量关系，进而求解。
易错点
审题错误（等差看成等比），或者由运算导致出错
知识点
在数列
18.求证：数列
19.若
正确答案
详见解析
解析
解：由
又
∴
考查方向
数列与不等式的综合；等差数列的通项公式
解题思路
已知等式两边同除anan+1化简后，根据等差数列的定义可证数列为等差数列，由等差数列的通项公式求出{an}的通项公式；
易错点
计算化简错误，数列相关性质掌握混淆
正确答案
详见解析
解析
法1:
∵
∴
设
∴当
∴
所以
法2
∵
∴
令
令
∴
考查方向
数列与不等式的综合；等差数列的通项公式
解题思路
由（Ⅰ）和分离常数法化简不等式，利用作差法判断数列的单调性，再求出t的取值范围
易错点
对数列的定义、通项公式等相关概念和性质掌握不牢
3．设{an}是等差数列，若log2a7=3，则a6+a8等于（ ）
正确答案
解析
由
考查方向
等差数列的性质
解题思路
由
易错点
计算
教师点评
等差数列的性质运算，属基础题
知识点
3.设
A
B
C
D
正确答案
解析
由
又
考查方向
等差数列的
解题思路
由
结合
易错点
教师点评
综合考查数列求和公式和性质的应用
知识点
7.已知数列
A
B
C
D
正确答案
解析
考查方向
等比数列的性质
解题思路
易错点
计算错误
教师点评
知识点
7.已知
A
B
C10
D12
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析