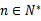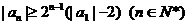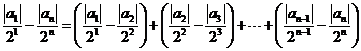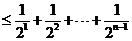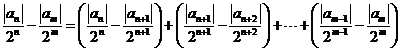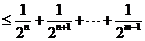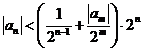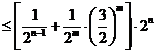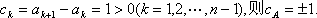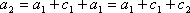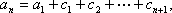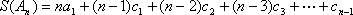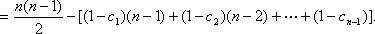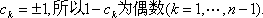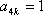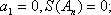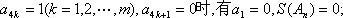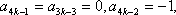- 数列与其它知识的综合问题
- 共8题
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分
若无穷数列




(1) 若







(2) 若无穷数列






(3) 设





正确答案
(1)
∴
∴
∴
∴
∴
(2)设



∴
∴
∴
∴
∴
∵
而

故
(3) 充分性:若
则
若存在

则
故
必要性:若对任意

则
设函数
由

∴一定能找到一个
∴
∴
故
∴
知识点
设数列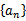
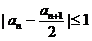
(Ⅰ)求证:
(Ⅱ)若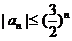
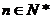
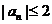
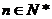
正确答案
(I)由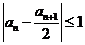
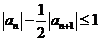
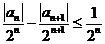

所以
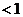
因此
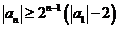
(II)任取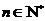
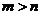
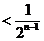
故
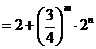
从而对于任意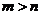
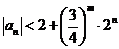
由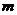
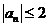
否则,存在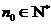
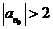
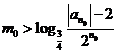
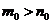
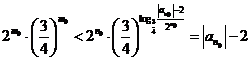
与①式矛盾.
综上,对于任意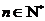
知识点
11. 无穷数列
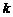
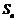
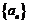
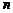
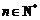
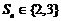
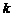
值为___________
正确答案
知识点
15.已知数列


正确答案
解析

所以

则


因为



又因为


考查方向
解题思路
1.先由


易错点
本题易在求通项用累加法时出现错误.
知识点
11. 对于数列










正确答案
16
解析
由






















考查方向
解题思路
1.先根据题中给出的条件求几项,后发现规律:若要使得



2.利用等差数列和等比数列的求和公式求出a,b后做差。
易错点
1.无法理解题中给出的条件
知识点
10.如果数列

















(参考数据:

正确答案
解析
由












所以数列









考查方向
解题思路
先利用条件求出数列


易错点
不会利用向量加法的几何意义运算或进行向量的数量积运算时,夹角出错,
知识点
已知复数






(1)求数列

(2)求和:①

正确答案
见解析
解析
解析:(1)


由







(2)①由(1)知






②当




又

知识点
若数列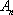
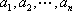
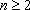
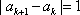
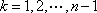
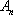
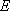
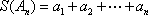
(1)写出一个满足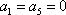
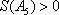
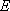
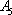
(2)若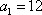
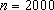
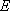
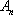
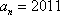
(3)对任意给定的整数
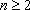
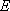
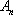
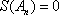
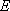
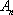
正确答案
见解析
解析
(1)0,1,2,1,0是一具满足条件的E数列A5。
(答案不唯一,0,1,0,1,0也是一个满足条件的E的数列A5)
(2)必要性:因为E数列A5是递增数列,
所以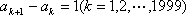
所以A5是首项为12,公差为1的等差数列.
所以a2000=12+(2000—1)×1=2011.
充分性,由于a2000—a1000≤1,
a2000—a1000≤1
……
a2—a1≤1
所以a2000—a≤19999,即a2000≤a1+1999.
又因为a1=12,a2000=2011, ∴a2000=a1+1999.
故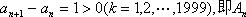
综上,结论得证。
(3)令
∵
……
∴
∵
∴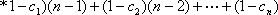
∴要使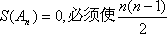
即4整除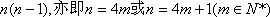
当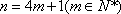
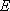
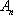
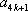

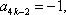
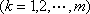
当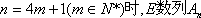
当
知识点
扫码查看完整答案与解析