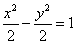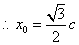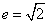直线与圆锥曲线的综合问题
共150题

· 直线与圆锥曲线的综合问题

直线与圆锥曲线的综合问题
共150题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

已知椭圆过点,离心率为.

（1）求椭圆的方程；

（2）过点且斜率为（）的直线与椭圆相交于两点，直线，分别交直线于，两点,线段的中点为.记直线的斜率为，求证: 为定值。

正确答案

见解析

解析

（1）依题得解得，.

所以椭圆的方程为. …………………………………………………4分

（2）根据已知可设直线的方程为.

由得.

设,则.

直线，的方程分别为：，

令，

则,所以.

所以

. ……………………………………………………14分

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题

题型：简答题

简答题 · 14 分

已知椭圆和点，垂直于轴的直线与椭圆交于两点，连结交椭圆于另一点.

（1）求椭圆的焦点坐标和离心率；

（2）证明直线与轴相交于定点.

正确答案

见解析

解析

（1）由题意知：所以

所以，焦点坐标为；离心率…………………4分

（2）由题意知：直线PB的斜率存在，设直线PB的方程为……………………5分

，，则，

由得

则 (1) ……………………8分

直线AE的方程为，令，得 (2) ……10分

又，代入(2)式，得 (3)

把(1)代入(3)式，整理得，所以直线AE与轴相交于定点. …………………14分

知识点

椭圆的几何性质直线与椭圆的位置关系直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题

题型：填空题

填空题 · 5 分

抛物线的焦点坐标为，则抛物线的方程为，若点在抛物线上运动，点在直线上运动，则的最小值等于（）.

正确答案

解析

略

知识点

抛物线的标准方程和几何性质直线与圆锥曲线的综合问题

题型：简答题

简答题 · 14 分

已知椭圆（）的焦点坐标为，离心率为，直线交椭圆于，两点。

（1）求椭圆的方程；

（2）是否存在实数，使得以为直径的圆过点？若存在，求出的值；若不存在，请说明理由。

正确答案

（1）

（2）

解析

（1）由，，得，，

所以椭圆方程是： ……………………4分

（2）设，则，

将代入，整理得（*）

则 ………………………7分

以PQ为直径的圆过，则，即

， ………………………………12分

解得，此时（*）方程，

所以存在，使得以为直径的圆过点， ……14分

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

题型：简答题

简答题 · 14 分

已知双曲线的右焦点为.

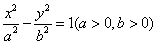
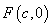
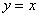
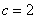
（1）若双曲线的一条渐近线方程为且，求双曲线的方程；

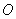
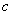
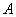
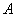
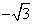
（2）以原点为圆心，为半径作圆，该圆与双曲线在第一象限的交点为，过作圆的切线，斜率为，求双曲线的离心率。

正确答案

见解析。

解析

解：（1）双曲线的渐近线方程为，，，，所求双曲线方程为

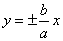
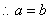
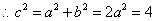
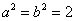
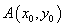
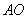
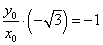
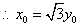
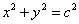
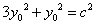
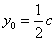
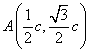
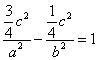
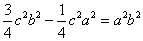
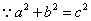
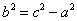
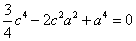
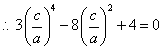
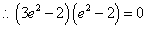
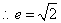
（2）设点，直线的斜率满足， ①，依题意，圆的方程为，将①代入圆的方程得：，即，，代入双曲线方程得：，即 ②，又，将代入②得：，，，或（舍去），故双曲线的离心率

知识点

双曲线的定义及标准方程双曲线的几何性质直线与圆锥曲线的综合问题

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 文科数学 > 直线与圆锥曲线的综合问题

扫码查看完整答案与解析