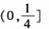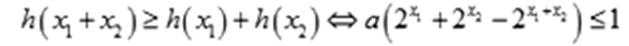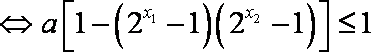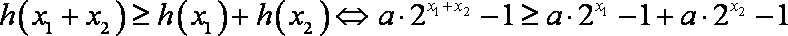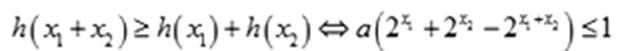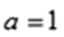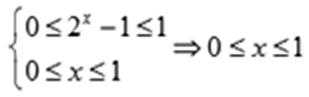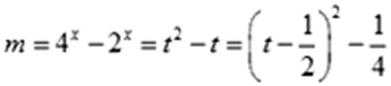- 函数零点的判断和求解
- 共165题
函数f（x）=（x﹣1）cosx2在区间[0，4]上的零点个数是（ ）
正确答案
解析
令f（x）=0，可得x=1或cosx2=0
∴x=1或x2=kπ+
∵x∈[0，4]，则x2∈[0，16]，
∴k可取的值有0，1，2，3，4，
∴方程共有6个解，
∴函数f（x）=（x﹣1）cosx2在区间[0，4]上的零点个数为6个，
故选C
知识点
定义在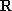
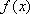
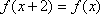
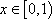
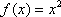
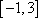
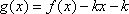
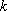
正确答案
解析
略
知识点
已知函数f（x）=||x﹣1|﹣1|，若关于x的方程f（x）=m（m∈R）恰有四个互不相等的实数根x1，x2，x3，x4，则x1x2x3x4的取值范围是 。
正确答案
（﹣3，0）
解析
函数f（x）=||x﹣1|﹣1|的图象如下图所示：
由图可知，若f（x）=m的四个互不相等的实数根，则m∈（0，1）
且x1，x2，x3，x4分别为：
x1=m，x2=2﹣m，x3=m+2，x4=﹣m，
∴x1x2x3x4=（m2）2﹣4•m2=（m2﹣2）2﹣4∈（﹣3，0）
知识点
定义在
正确答案
1207
解析
由
知识点
已知函数
若关于
A
B
C
D
正确答案
解析
略
知识点
已知定义在实数集
A
B
C
D
正确答案
解析
略
知识点
对定义在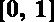
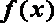
① 对任意的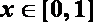
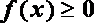
② 当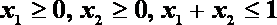
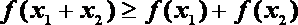
已知函数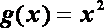
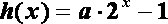
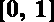
（1）试问函数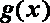
（2）若函数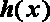
（3）在（2）的条件下，若方程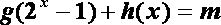
正确答案
见解析
解析
（1）当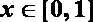
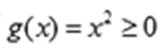
当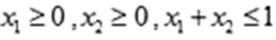
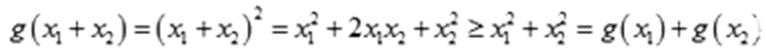
所以函数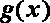
（2）因为函数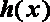
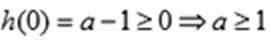
根据②有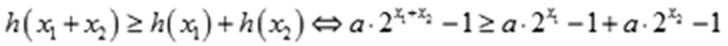
因为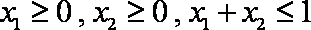
所以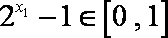
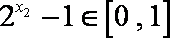
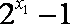
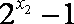
于是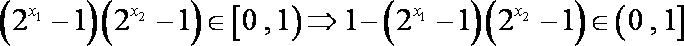
所以
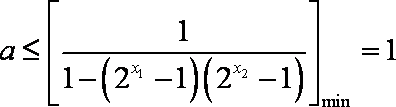
于是
另解：因为函数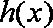
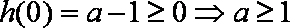
根据②有
取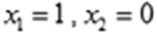
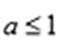
（3）根据（2）知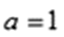
由
令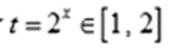
因此，当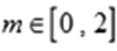
知识点
已知偶函数
正确答案
（
解析
略
知识点
5.函数
正确答案
解析
函数
知识点
9．函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析