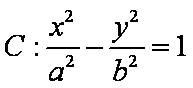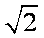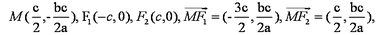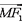- 直线与抛物线的位置关系
- 共38题
已知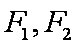
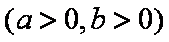
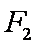
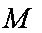
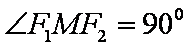
正确答案
解析
∵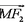
知识点
已知双曲线




正确答案
-2
解析
略
知识点
为了了解某年级1 000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,被抽取学生的成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组

(1)将频率当作概率,请估计该年级学生中百米成绩在
(2)求调查中随机抽取了多少名学生的百米成绩;
(3)若从第一、五组中随机取出两名学生的成绩,求这两名学生的成绩的差的绝对值大于1的概率。
正确答案
见解析。
解析
(1)百米成绩在


所以估计该年级学生中百米成绩在
(2)设图中从左到右的前3个组的频率分别为
依题意,得

设调查中随机抽取了


故调查中随机抽取了50名学生的百米成绩,(8分)
(3)百米成绩在第一组的学生人数为

百米成绩在第五组的学生人数为

则从第一、五组中随机取出两名学生的成绩包含的基本事件有:




















其中满足成绩的差的绝对值大于1的基本事件有:











所以所求概率
知识点
与直线x+2y+3=0垂直,且与抛物线y = x2 相切的直线方程是 。
正确答案
解析
略
知识点
已知极坐标系的极点为直角坐标系


(1)求
(2)直线






正确答案
见解析。
解析
(1)
则


(2)将


设点


知识点
扫码查看完整答案与解析