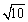- 求线性目标函数的最值
- 共187题
约束条件
正确答案
2
解析
不等式组所表示的平面区域如图所示
解得A(2,0)、B(0,2)、O(0,0),
所以S△ABO=
表示的平面区域的面积为:2。
知识点
设




(1)k的值为
(2)
正确答案
1;7
解析
作出不等式组表示的平面区域,由题意可知直线 
当直线


知识点
设变量x,y满足|x|+|y|≤1,则x+2y的最大值为 _________ 。
正确答案
2
解析
约束条件|x|+|y|≤1可化为:
其表示的平面区域如图所示的正方形及内部:
设目标函数z=x+2y,变形可得y=
经平移直线可知当直线经过点(0,1)时z=x+2y取最大值2
知识点
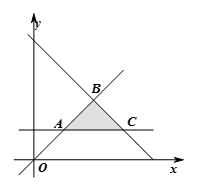
已知点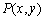
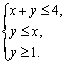
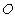
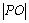
正确答案
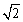
解析
做出可行域,由条件知,可行域为三角形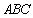
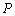
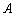
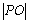
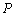
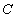
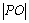
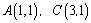
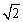
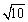
知识点
将容器为n的样本中的数据分成6组,绘制频率分布直方图,若第一组至第六组数据的频率之比为
正确答案
60
解析
知识点
目标函数z=3x+y在约束条件
正确答案
9
解析
作出不等式组
得到如图的△ABC及其内部,其中A(


设z=F(x,y)=3x+y,将直线l:z=3x+y进行平移,
当l经过点B时,目标函数z达到最大值
∴z最大值=F(3,0)=9
故答案为:9
知识点
某工厂为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的维护费用会逐年增加,第1年的维护费用是4万元,从第2年到第7年,每年的维护费用均比上年增加2万元,从第8年开始,每年的维护费用比上年增加25%。
(1)设第n年该生产线的维护费用为an,求an的表达式;
(2)设该生产线前n年的维护费用为Sn,求Sn.
正确答案
见解析
解析
(1)由题意知,当n≤7时,数列{an}是首项为4,公差为2的等差数列,
故an=4+(n-1)×2=2n+2. …………………..2分
当n≥8时,数列{an}从a7开始构成首项为a7=2×7+2=16,公比为1+25%=的等比数列,
则此时an=16×n-7,……………5分
所以an=..........6分
(2)当1≤n≤7时,Sn=4n+×2=n2+3n,……………..8分
当n≥8时,由S7=70,得Sn=70+16××=80×n-7-10,…………10分
所以该生产线前n年的维护费用为
Sn=...........13分
知识点
设:x,y满足约束条件

正确答案
解析
作图,满足约束条件
4个顶点是(0,0),(0,2),(1/2,0),(1,4),
由图易得目标函数在(1,4)取最大值8,即8=ab+4∴ab=4,
∴a+b≥2
故答案为:4
知识点
如图,圆














(1)求证:
(2)求
正确答案
见解析
解析
解法一:
(1)连接

即



∴
又



∴
∴
(2)∵
∴



∴


解法2:
(1)连接

∴
∵

(2)∵

∴


即
又∵
∴
知识点
已知实数


正确答案
-4
解析
当x=2,y=3,x-2y取得最小值-4.
知识点
扫码查看完整答案与解析