- 等比数列
- 共373题
2.已知等比数列{an}中,

正确答案
解析




考查方向
解题思路
1)将

2)求
3)将
易错点
本题易在运算上出现错误,也容易按等差数列的性质做题.
知识点
13.各项为正数的等比数列




正确答案
解析
由




考查方向
解题思路
本题考查等比数列的性质及对数的运算法则。
易错点
不记得等比数列的性质。
知识点
17.
已知{an}是公差为3的等差数列,数列{bn}满足b1=1,b2=
(Ⅰ)求{an}的通项公式; (Ⅱ)求{bn}的前n项和.
正确答案
1
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
若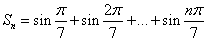
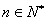
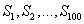
正确答案
解析
依据正弦函数的周期性,可以找其中等于零或者小于零的项.
知识点
盒子中装有编号为1,2,3,4,5,6,7的七个球,从中任意取出两个,则这两个球的编号之积为偶数的概率是______(结果用最简分数表示)。
正确答案
解析
从4个奇数和3个偶数共7个数中任取2个,共有




知识点
等差数列{an}中,a7=4,a19=2a9.
(1)求{an}的通项公式;
(2)设
正确答案
见解析。
解析
(1)设等差数列{an}的公差为d,则
an=a1+(n-1)d.
因为
所以
解得a1=1,
所以{an}的通项公式为
(2)因为
所以
知识点
已知等差数列{an}满足:a1=2,且a1,a2,a5成等比数列。
(1)求数列{an}的通项公式;
(2)记Sn为数列{an}的前n项和,是否存在正整数n,使得Sn>60n+800?若存在,求n的最小值;若不存在,说明理由。
正确答案
见解析。
解析
(1)设数列{an}的公差为d,依题意,2,2+d,2+4d成比数列,故有(2+d)2=2(2+4d),
化简得d2﹣4d=0,解得d=0或4,
当d=0时,an=2,
当d=4时,an=2+(n﹣1)•4=4n﹣2。
(2)当an=2时,Sn=2n,显然2n<60n+800,
此时不存在正整数n,使得Sn>60n+800成立,
当an=4n﹣2时,Sn=
令2n2>60n+800,即n2﹣30n﹣400>0,
解得n>40,或n<﹣10(舍去),
此时存在正整数n,使得Sn>60n+800成立,n的最小值为41,
综上,当an=2时,不存在满足题意的正整数n,
当an=4n﹣2时,存在满足题意的正整数n,最小值为41
知识点
3.设{an}是等差数列,若log2a7=3,则a6+a8等于( )
正确答案
解析
由

考查方向
等差数列的性质
解题思路
由

易错点
计算
教师点评
等差数列的性质运算,属基础题
知识点
13.若三个正数





正确答案
1
解析
因为三个正数






知识点
扫码查看完整答案与解析






