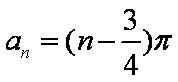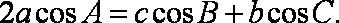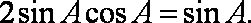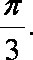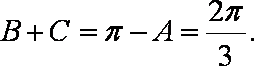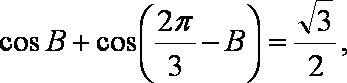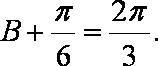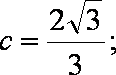- 等比数列
- 共373题
在数列









(1)求证:
(2)设


正确答案
见解析。
解析
(1)由



由



①

所以

(2)由(1)知,
①

③

代入

所以
整理得,
所以
由

所以

当



当



故使



知识点
函数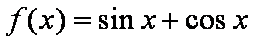

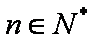
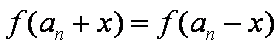
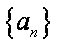
正确答案
解析
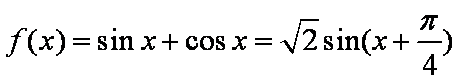
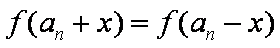
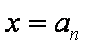
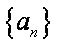
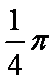
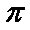
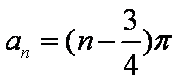
知识点
已知数列





(1)求证:数列

(2)设数列











正确答案
见解析。
解析
(1)因为

则
所以
又




即

(2)由(1)知

①当



若




因为




所以(
②当



则

即

欲满足题设条件,只需

因为


即
综上所述,当


当


知识点
已知实数a、b、c、d成等比数列,且函数
正确答案
解析
y′=-1,令y′=0得x=-1,当-2<x<-1时,y′>0,当x>-1时,y′<0,∴b=-1,c=ln(-1+2)-(-1)=1,∴ad=bc=-1,故选A
知识点
在数列


(1)求数列
(2)求证:数列
(3)设数列



正确答案
见解析。
解析
(1)



∴
(2)
∴
∴
∴数列


(3)由(1)知,
∴
∴
……………………………10分

知识点
若等比数列{an}满足am﹣3=4且
正确答案
16
解析
∵数列{an}为等比数列,amam﹣4=
∴m﹣4,4,m成等差数列,
∴m+(m﹣4)=8,
解得:m=6。
∴am﹣3=a3=4。
又a1,a3,a5成等比数列,
∴a1a5=
知识点
已知集合









(1)求数列
(2)若数列


正确答案
见解析。
解析
(1)由题设知: 集合





由此可得,对任意的



设等差数列


因为

由于


所以

所以数列


(2)
于是有

知识点
已知数列


有
(1)求证:对一切
(2)求数列
(3)求证:
正确答案
见解析。
解析
(1) 证明: 

② - ①:



(2)解:由
两式相减,得:


(3)证明: ∵
∴
∴
知识点
在△ABC中,角A,B,C的对边分别是a,b,c,已知
(1)求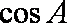
(2)若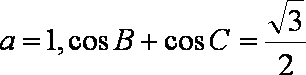
正确答案
见解析。
解析
(1)由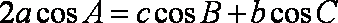
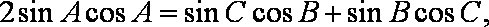
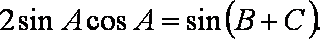
又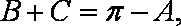
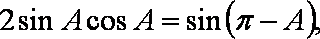
而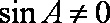
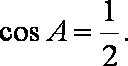
(2)由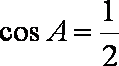
因此
由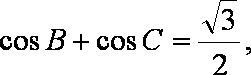
即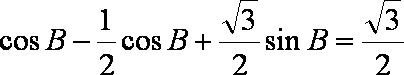
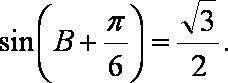
由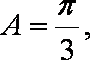
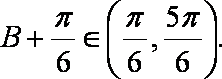
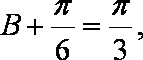
所以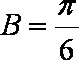

若
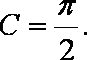
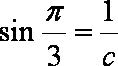
若
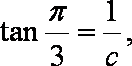
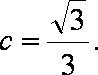
知识点
已知等差数列{an}中,a3=-4,a1+a10=2,
(1)求数列{an}的通项公式;
(2)若数列{bn}满足an=log3bn,设Tn=b1·b2……bn,当n为何值时,Tn>1。
正确答案
见解析。
解析
(1)设数列{an}的公差为d,则
解之得
(2)
知识点
扫码查看完整答案与解析