- 等比数列
- 共373题
8.已知{an}是等差数列,Sn是其前n项和.若a1+a22=
正确答案
20
知识点
15.设数列



正确答案
15
解析
数列



+2+4+8=15.
考查方向
解题思路
分别计算出每一项,再相加即可。
易错点
弄错符号。
知识点
10.设





正确答案
解析
设等比数列


考查方向
解题思路
利用等比数列的性质,将
易错点
1、等比数列求和的性质不能正确使用,注意的是“片段和”,而不是“和”。
2、本题不容易联系到基本不等式,并正确地使用不等式:一正二定三相等。
知识点
14.各项均为正数的等比数列



正确答案
解析
试题分析:由




考查方向
解题思路
直接利用等比数列的通项公式进行计算。
易错点
相关知识点不熟悉导致出错。
知识点
7. 已知等比数列



正确答案
解析
由


考查方向
解题思路
由

易错点
公比的正负情况不知道。
知识点
12.



且

正确答案
8
解析


所以

所以

所以填8
考查方向
解题思路
先求出a7的值,然后再求答案
易错点
不转换建立关系,直接算
知识点
6.在正项等比数列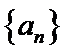
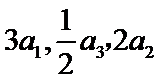
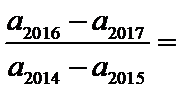
正确答案
解析
由题可知:a3=3a1+2a2,即a1q2=3a1+2a1q,解得q=-1(舍去)或q=2.a2016=a2014q2,
a2017=a2014q3,a2015=a2014q,约分即可。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
1、求出q;
2、代入计算,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在求q时发生错误。
知识点
3.若实数数列:

正确答案
解析
由


考查方向
本题主要考查等比数列的概念和椭圆的离心率的概念。
解题思路
由等比数列求出a,代入圆锥曲线方程求出离心率。
易错点
1、等比数列概念不清导致a 漏负解
2、误认为圆锥曲线只是椭圆导致漏解。
知识点
17.设数列




(1)求数列

(2)设



正确答案
(1)

(2)
解析
(1)



(2)
两式相减得
考查方向
本题主要考查了数列的通项公式和求和
解题思路
(1)利用
(2)利用错位相减法求出前n项和本题考查导数的性质,
易错点
(1)利用定义求通项公式
(2)第二问中错位相减法计算的准确性;
知识点
6.设


正确答案
解析
根据题意知,


考查方向
本题主要考查了等比数列与均值不等式的综合应用,在近几年的各省高考题出现的频率较高,常与数列、不等式等知识点交汇命题。
易错点
均值不等式取等条件容易忽视。
知识点
扫码查看完整答案与解析























