- 双曲线的定义及标准方程
- 共311题
1
题型:简答题
|
正确答案
见解析
解析
(1)原曲线方程可化简得:
由题意可得:
(2)由已知直线代入椭圆方程化简得:

由韦达定理得:

设






欲证


即
将①②代入易知等式成立,则
知识点
双曲线的定义及标准方程
1
题型:填空题
|
已知点F,B分别为双曲线C:
正确答案
解析
略
知识点
双曲线的定义及标准方程
1
题型:填空题
|
设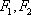
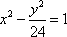
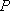
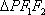
正确答案
24
解析
略
知识点
双曲线的定义及标准方程
1
题型:
单选题
|
已知双曲线

正确答案
A
解析
略
知识点
双曲线的定义及标准方程
1
题型:简答题
|
已知椭圆C的一个焦点在抛物线 


(1)求椭圆C的方程;
(2)设过点M(2,0)的直线与椭圆C相交于两点A、B,满足 

正确答案
见解析
解析
知识点
双曲线的定义及标准方程
下一知识点 : 双曲线的几何性质
扫码查看完整答案与解析













