- 函数模型的选择与应用
- 共46题
11.受2008年国际金融危机的影响,某企业单位在人事制度改革中对员工进行分流,被分流的入员当年可在原单位领取原工资的100%,从第二年起每年只在原单位领取前一年工资的



正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
19.因发生意外交通事故,一辆货车上的某种液体泄露到一鱼塘中。为治理污染,根据环保部门的建议,现决定在鱼塘中投放一种可与污染液体发生化学反应的药剂。已知每投放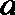
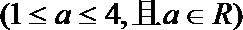
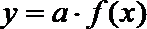
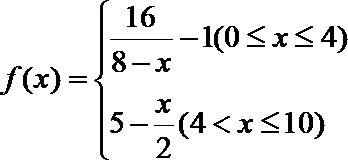
(1)若一次投放4个单位的药剂,则有效治污的时间可达几天?
(2)若因材料紧张,第一次只能投放2个单位的药剂,6天后再投放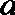
正确答案
(1)因为 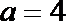
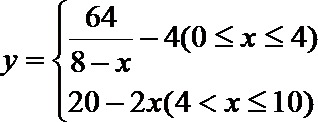
①当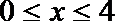
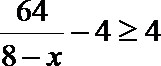
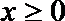
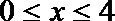
②当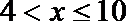
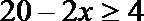
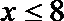
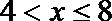
综合得,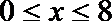
(2) 当
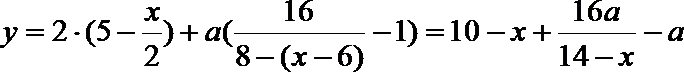
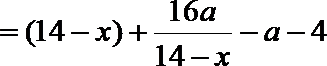
由题意知,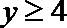
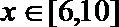
因为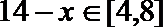
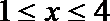
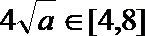
故当且仅当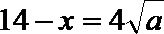
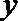

令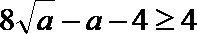
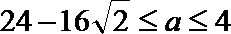
又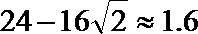
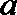
解析
解析已在路上飞奔,马上就到!
知识点
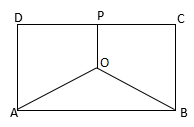
17.某地有三家工厂,分别位于矩形ABCD的顶点A、B及CD的中点P处,已知AB=20km,BC=10km,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A、B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP,设排污管道的总长为ykm。
(1)按下列要求写出函数关系式:
①设∠BAO=θ(rad),将y表示成θ的函数关系式;
②设OP=x(km),将y表示成x的函数关系式;
(2)请你选用(1)中的一个函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某人准备购置一块占地



(1)试用

(2)若要使

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 某商场在店庆一周年开展“购物折上折活动”:商场内所有商品按标价的八折出售,折后价格每满500元再减100元。如某商品标价为1500元,则购买该商品的实际付款额为1500×0.8-200=1000(元)。设购买某商品得到的实际折扣率=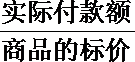
(1)写出当x∈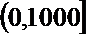
(2)对于标价在[2500,3500]的商品,顾客购买标价为多少元的商品,可得到的实际折扣率低于
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.为了研究某种药物,用小白鼠进行试验,发现药物在血液内的浓度与时间的关系因使用方式的不同而不同。若使用注射方式给药,则在注射后的3小时内,药物在白鼠血液内的浓度




(1)若a=1,求3小时内,该小白鼠何时血液中药物的浓度最高,并求出最大值?
(2)若使小白鼠在用药后3小时内血液中的药物浓度不低于4,求正数a的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某校为扩大教学规模,从今年起扩大招生,现有学生人数为b人,以后学生人数年增长率为4.9‰.该校今年年初有旧实验设备a套,其中需要换掉的旧设备占了一半。学校决定每年以当年年初设备数量的10%的增长率增加新设备,同时每年换掉x套的旧设备。
(1)如果10年后该校学生的人均占有设备的比率正好比目前翻一番,那么每年应更换的旧设备是多少套?
(2)依照(1)的更换速度,共需多少年能更换所有需要更换的旧设备?
下列数据供计算时参考:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某出版社新出版一本高考复习用书,该书的成本为5元一本,经销过程中每本书需付给代理商




(1)求该出版社一年的利润L(万元)与每本书的定价
(2)若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在计量某种物品的重量x(1≤x<100)时,规定仅取整数值y,由于该种物品的特殊性,要求按五舍六入的办法进行(即用x除以10的余数大于6时进1,否则直接舍去),那么y与x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为( )
正确答案
解析
设x=10m+α(0≤α≤9),
当0≤α≤6时,
当6<α≤9时,
所以选B.
知识点
21.节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形














(1)将

(2)试确定
正确答案
(1)

(2)点





解析
(1)由已知得
即

(2)记


解得

由于







考查方向
本题以实际问题为背景,主要考查函数解析式的构建以及函数最值的求解,考查数学建模的能力,是中档题.以实际问题为背景的生活中的优化问题,这类问题在近几年各省市的高考试卷中频频出现,是高考的热点问题.这类问题往往涉及到建立函数关系式和函数的最值,一般先设自变量、因变量,建立函数关系式,并确定其定义域,求最值时可利用三角函数的有界性、函数的单调性,也可直接利用导数求最值,要掌握求最值的方法和技巧.也注意结果应与实际情况相符合.
解题思路
先建立函数,再利用三角函数的有界性求
易错点
建立函数过程中,容易遗忘定义域,还要注意实际情况;求最值的有多种方法,还要注意结果应与实际情况相符合.
知识点
扫码查看完整答案与解析