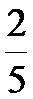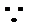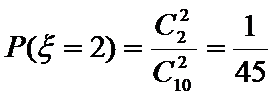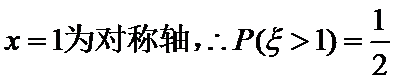- 正态分布曲线的特点及曲线所表示的意义
- 共26题
13.已知随机变量X服从正态分布X~N(2,σ2), P(X<4)=0.84, 则P(X≤0)的值为 .
正确答案
解析
考查方向
本题考查的是正态分布,属于基础题。近年高考常考,需要注意。
解题思路
本题考查的主要是正态分布,先求出
易错点
本题在画正态分布图时易错,导致
教师点评
本题考查了正态分布,近年常在填空题中,和解答题中穿插出现,属于简单题,但是由于复习中用的课时比较少,所以必须加强复习
知识点
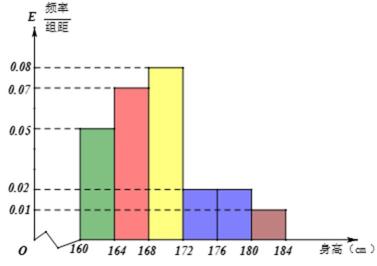
18.某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160 cm和184 cm之间,将测量结果按如下方式分成6组:第一组 [160,164],第二组[164,168],…,第6组[180,184],下图是按上述分组方法得到的频率分布直方图.
(Ⅰ)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(Ⅱ)求这50名男生身高在172 cm以上(含172 cm)的人数;
(Ⅲ)在这50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全市前130名的人数记为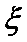
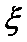
参考数据:若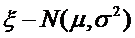
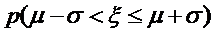
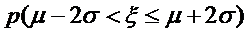
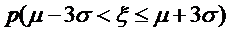
正确答案
(Ⅰ)平均值168.72,高于全市平均值
(Ⅱ)10人.
(Ⅲ)
解析
(Ⅰ)由直方图,经过计算该校高三年级男生平均身高为
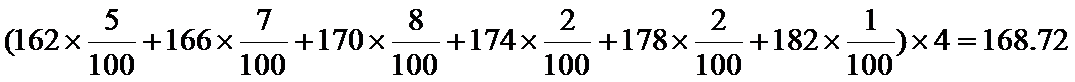
高于全市的平均值168(或者:经过计算该校高三年级男生平均身高为168.72,比较接近全市的平均值168).
(Ⅱ)由频率分布直方图知,后三组频率为(0.02+0.02+0.01)×4=0.2,人数为0.2×50=10,即这50名男生身高在172 cm以上(含172 cm)的人数为10人.
(Ⅲ)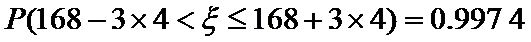
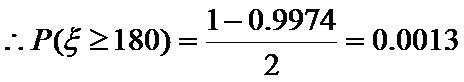
所以,全市前130名的身高在180 cm以上,这50人中180 cm以上的有2人.
随机变量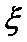
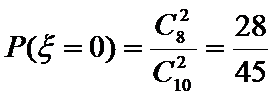
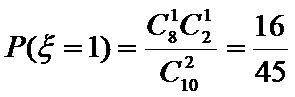
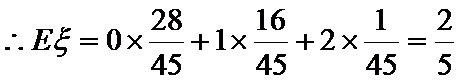
考查方向
解题思路
第一问估算,直接用每组的平均值乘以频率,然后相加即得
第二问先计算后三组的频率和,然后乘以总人数即得
第三问先根据正态分布概率计算出全市前130名是在那个身高区间,然后再计算50个人中有几个在这个区间,最后根据组合数计算出各变量的期望值,再相加即得。
易错点
1、对频率分布直方图认识不清,误把纵坐标当概率
2、对正态分布的意义理解不正确,不能正确计算概率
知识点
6.在如图所示的正方形中随机投掷10 000 个点,则落入阴
正确答案
解析
由正态分布N(-1,1)可知,





考查方向
解题思路
1.先利用正态分布求出阴影部分的面积;
2.利用几何概型的概率公式估计落入阴
易错点
1.不理解正态分布的知识导致无法入手;
2.对于几何概型的面积不理解导致出错。
知识点
3. 设随机变量ξ服从正态分布


正确答案
解析
由正态分布曲线可知,


考查方向
解题思路
根据正态分布曲线可知,数学期望是
易错点
对正态分布曲线不熟悉导致出错;不清楚


知识点
3.设随机变量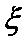
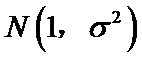
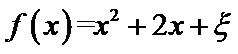
正确答案
解析
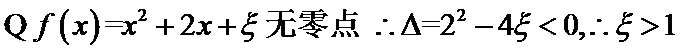
考查方向
解题思路
【解题思路】本题属于简单题,可使用直接法,
易错点
该题容易忽视正态分布曲线的对称性
知识点
扫码查看完整答案与解析