- 牛顿运动定律的应用-连接体
- 共42题
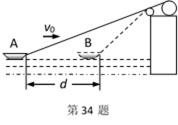
如图所示,斜面体固定在水平地面上,虚线以上部分斜面光滑,虚线以下部分斜面粗糙。质量分别为m1、m2(m2>m1)的两物体之间用细线连接,开始时m1处在斜面顶端并被束缚住。当由静止释放m1后,两物体开始沿斜面下滑。则下列说法正确的是
正确答案
解析
略。
知识点
如图所示,将斜面体固定在水平面上,其两个斜面光滑,斜面上放置一质量不计的柔软薄纸带(斜面上加粗部分为纸带)。现将质量为mA的A物体和质量为mB的B物体轻放在纸带上。两物体可视为质点,物体初始位置及数据如图所示。
(1)若纸带与物体A、B间的动摩擦因数足够大,在纸带上同时放上A、B后,发现两

(2)若mA=2 kg,mB=1 kg,A与纸带间的动摩擦因数μA=0.5,B与纸带间的动摩擦因数μB=0.8,假设两物体与纸面间的滑动摩擦力与最大静摩擦力相等,试通过计算简要描述两物体同时从静止释放后的运动情况,并求出B物体自释放起经过多少时间到达斜面底端。(sin37°=0.6,cos37°=0.8,g取10 m/s2)
正确答案
见解析
解析
(1)纸带处于平衡态,说明A、B两物体对纸带的静摩擦力大小相等,则

解得:
知识点
如图所示,用跨过光滑滑轮的缆绳将海面上一艘失去动力的小船沿直线拖向岸边,已知拖动缆绳的电动机功率恒为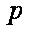
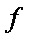
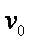
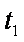
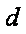
(1)A到B点过程中,小船克服阻力所做的功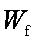
(2)小船经过B点时速度大小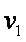
(3)小船经过B点时的加速度大小。
正确答案
见解析
解析
(1)小船从A点运动到B点克服阻力做功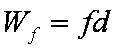
(2)小船从A点运动到B点,电动机牵引绳对小船做功W=Pt1 ②
由动能定理有 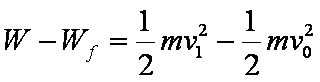
由①②③式解得 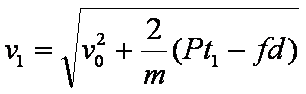
(3)设小船经过B点时绳的拉力大小为F,绳与水平方向夹角为θ,绳的速度大小为u,
P=Fu ⑤
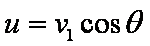
牛顿第二定律 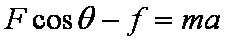
由④⑤⑥⑦得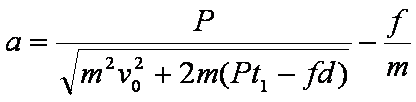
(另解:设细绳的拉力为F,绳与水平方向夹角为θ,则细绳牵引小船的功率为P=Fcosθ·v1
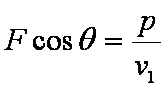
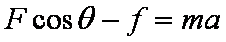
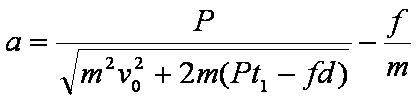
知识点
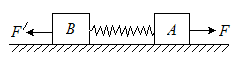
如图所示,在水平地面上有A、B两个小物体,质量分别为mA=3kg、mB=2kg,它们与地面间的动摩擦因数均为μ=0.1。A、B之间有一原长为L=0.15m、劲度系数为k=500N/m的轻质弹簧水平连接。分别用两个方向相反的水平恒力F、F'同时作用在A、B两物体上。当运动达到稳定时,A、B两物体以共同加速度大小为a=1m/s2做匀加速直线运动。已知F=20N,g取10m/s2。求运动稳定时A、B之间的距离及F'的大小。
正确答案
见解析
解析
当系统具有水平向右的加速度a=1m/s2时:设运动稳定时弹簧的伸长量为Δx1,A、B间距为L1,F'的大小为F1。
对A,有:F-kΔx1-μmAg=mAa ① ……………(2分)
对整体,有:F-μ(mA+mB)g-F1=(mA+mB)a ②……………(2分)
又有 L1=L+Δx1 ③ ……………(2分)
解得 F1=10N ④ ……………(1分)
L1=0.178m ⑤ ……………(1分)
当系统具有水平向左的加速度a=1 m/s2时:设运动稳定时弹簧的伸长量为Δx2,A、B间距为L2,F'的大小为F2。
对A,有:kΔx2-μmAg-F=mAa ⑥ ……………(1分)
对整体,有:F2-μ(mA+mB)g-F=(mA+mB)a ⑦……………(1分)
又有 L2=L+Δx2 ⑧ …………………… ……(1分)
解得 F2=30N ⑨ …………………… ……(1分)
L2=0.202m ⑩… …………………… ……(1分)
知识点
9.如图,升降机内有一固定斜面,斜面上放一物体,开始时升降机做匀速运动,物块相对斜面匀速下滑,当升降机加速上升时( )
A.物块与斜面间的摩擦力减小
B.物块与斜面间的正压力增大
C.物块相对于斜面减速下滑
D.物块相对于斜面匀速下滑
正确答案
B;D
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析