- 牛顿运动定律的应用-连接体
- 共42题
如图所示,质量M=8kg的长木板放在光滑水平面上,在长木板的右端施加一水平恒力F=8N,当长木板向右运动速率达到v1=10m/s时,在其右端有一质量m=2kg的小物块(可视为质点)以水平向左的速率v2=2m/s滑上木板,物块与长木板间的动摩擦因数μ=0.2,小物块始终没离开长木板,
(1)经过多长时间小物块与长木板相对静止;
(2)上述过程中长木板对小物块摩擦力做的功.
正确答案
(1)8s
(2)192J
解析
(1)小物块的加速度为:a2=μg=2m/s2, 水平向右
长木板的加速度为:
令刚相对静止时他们的共同速度为v,以木板运动的方向为正方向
对小物块有:v=-v2+a2t
对木板有:v= v1+a1t
代入数据可解得:t=8s;v=14m/s
(2)长木板对小物块摩擦力做的功为
知识点
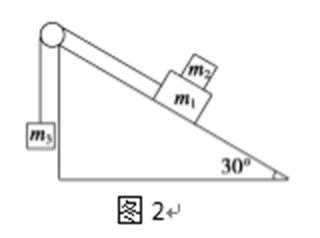
15.如图2所示,三个物体质量分别为m1=1.0kg、m2=2.0kg、m3=3.0kg,已知斜面上表面光滑,斜面倾角θ=30°,m1和m2之间的动摩擦因数μ=0.8.不计绳和滑轮的质量和摩擦.初始用外力使整个系统静止,当撤掉外力时,m2将(g=10m/s2,最大静摩擦力等于滑动摩擦力)( )
正确答案
解析
略
知识点
25. 如图所示,质量分别为


(1) 重物A自由下落的高度h
(2) 从弹簧开始被压缩到重物B离开水平地面的过程中,水平地面对重物B的最大支持力。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图所示,一木板静止在光滑水平面上,一木块从小车左端开始以速度v沿木板表面滑动。若将木板固定住,滑到木板右端木块克服摩擦力做的功为W1,产生的热量为Q1,运动时间为t1;若木板不固定,滑到木板右端木块克服摩擦阻力做的功为W2,产生的热量为Q2,运动时间为t2则 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如下图所示,放在水平地面上的物体M上叠放着物体

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析