- 直线与圆相交的性质
- 共47题
在直角坐标系








线

正确答案
考查方向
易错点
参数方程应用过程中的理解上易出错。
知识点
6.已知圆的方程为
正确答案
解析
由垂径定理可知:当点(3,5)为弦中点时为最短弦


考查方向
本题主要考查了点圆关系,当点在圆内时,过此点的最长弦与最短弦。在近几年的各省高考题出现的频率较高,直线与圆的位置关系一般在小题里考,也常与线性规划和均值不等式联系。
易错点
对这个模型不太熟悉,即垂径定理的应用。
知识点
20. 已知点M(-1,0),N(1,0),曲线E上任意一点到点M的距离均是到点N距离的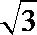
(Ⅰ)求曲线E的方程;
(Ⅱ)已知m≠0,设直线l1:x-my-1=0交曲线E于A,C两点,直线l2:mx+y-m=0交曲线E于B,D两点.C,D两点均在x轴下方.当CD的斜率为-1时,求线段AB的长.
正确答案
(1)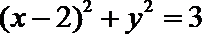
(2)线段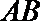
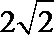
解析
⑴解:设曲线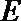
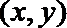
由题意,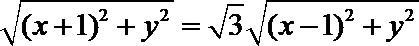
整理得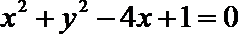
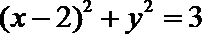
⑵解:由题知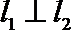
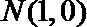
设曲线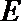
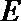
则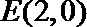
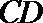
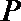
则直线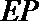
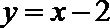
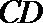
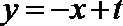
由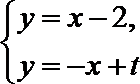
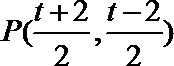
由圆的几何性质,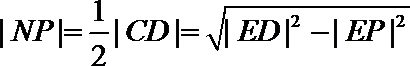
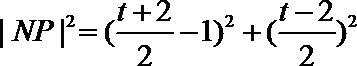
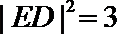
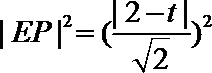
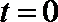
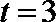
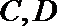
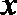
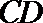
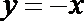
解得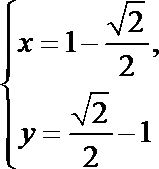

设
由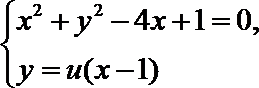

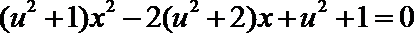
⑴ 方程⑴的两根之积为1,
所以点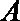
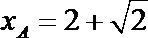
又因为点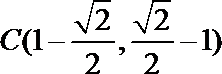
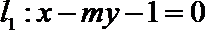
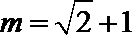
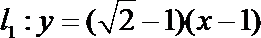
所以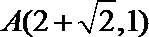
同理可得,
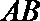
考查方向
本题考查了圆的标准方程和直线与圆的位置关系,属于高考中的高频考点.
解题思路
1、利用已知求解。
2、联立直线与圆方程求解。
易错点
第二问中表示直线斜率时容易出错。
知识点
7.过三点A(1,3),B(4,2),C(1,-7)的圆交于y轴于M、N两点,则
正确答案
知识点
18.已知直线


(1)


(2)直线


正确答案
(2)
解析
(1)直线总过定点


(2)
考查方向
本题考查了直线系方程的应用以及直线与圆相交等知识。
解题思路
(1)运用直线系的方程,找到直线所过的定点。
(2)运用直线与圆相交的性质求出弦长。
易错点
第二问不知道弦与半径所在直线垂直的时候弦长最短,从而得不到正确答案。
知识点
扫码查看完整答案与解析