- 指数函数的图像与性质
- 共51题
已知函数


(1)求函数
(2)若函数


正确答案
见解析
解析
解析:(1)∵
∴
由





∴单调递增区间为
(2)







当


知识点
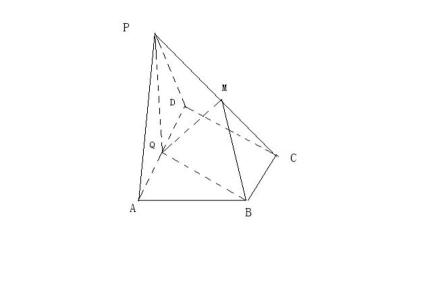
如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD垂直底面。Q为AD中点,M是棱PC上的点,PA=PD=2,BC=
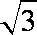
(1)若点


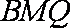
(2)求证:平面PQB
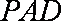
(3)若二面角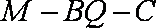
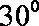
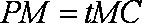
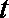
正确答案
见解析
解析
(1)在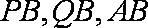


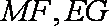
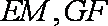
因为底面ABCD为直角梯形,AD∥BC,∠ADC=90°,BC=
于是有: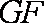
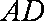


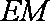
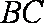
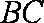
所以,四边形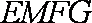
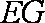
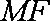

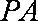
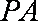
所以,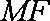
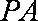
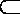
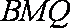

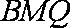
(2)证明:由已知条件得:
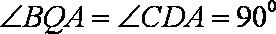
即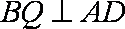
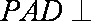


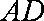
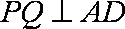
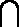
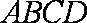
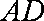
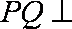
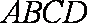
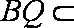
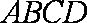
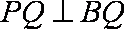
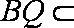
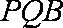
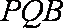

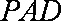
(3)平面PAD⊥底面,而PAD是正三角形,Q为AD中点,
所以PQ⊥AD,PQ⊥底面ABCD,连接CQ,做MN⊥CQ,做NE⊥QB,连ME
MN⊥CQ,PQ⊥CQ,所以MN∥PQ
MN/PQ=CM/CP=1/(1+t) MN=√3/(1+t)
而容易看到BCQD是矩形,NE⊥BQ,所以NE∥BC
NE/BC=QN/QC=t/(1+t) NE=t/(1+t)
二面角就是∠MEN
tan∠MEN=MN/NE=√3/(1+t)/t/(1+t)=√3/t
所以t=3.
知识点
直线



正确答案
解析
圆的方程化为


知识点
已知实数x,y满足
正确答案
[-3,1]
解析
令


在
易知直线


直线

因此
知识点
在直三棱柱ABC﹣A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上。
(1)求证:BC⊥A1B;
(2)若
正确答案
见解析。
解析
(1)证明:三棱柱 


又


又











又



(2)在直三棱柱







在



在

由(1)知








知识点
扫码查看完整答案与解析