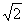直线的斜截式方程
共7题

· 直线的斜截式方程

直线的斜截式方程
共7题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

7.已知圆M：截直线所得线段的长度是，则圆M与圆N：的位置关系是

A内切

B相交

C外切

D相离

正确答案

知识点

直线的斜截式方程

题型：单选题

单选题 · 5 分

若，则称点在抛物线C：外，已知点在抛物线C：外，则直线与抛物线C的位置关系是（　　）

A相交

B相切

C相离

D不能确定

正确答案

解析

略

知识点

直线的斜截式方程

题型：单选题

单选题 · 5 分

若直线过圆的圆心,则a的值为

正确答案

解析

略

知识点

直线的斜截式方程

题型：简答题

简答题 · 12 分

已知圆M：(x＋1)2＋y2＝1，圆N：(x－1)2＋y2＝9，动圆P与圆M外切并且与圆N内切，圆心P的轨迹为曲线C.

（1）求C的方程；

（2）l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P的半径最长时，求|AB|。

正确答案

（1）(x≠－2)

（2）|AB|＝或|AB|＝

解析

由已知得圆M的圆心为M(－1,0)，半径r1＝1；圆N的圆心为N(1,0)，半径r2＝3.设圆P的圆心为P(x，y)，半径为R.

（1）因为圆P与圆M外切并且与圆N内切，

所以|PM|＋|PN|＝(R＋r1)＋(r2－R)＝r1＋r2＝4.

由椭圆的定义可知，曲线C是以M，N为左、右焦点，长半轴长为2，短半轴长为的椭圆(左顶点除外)，其方程为(x≠－2)。

（2）对于曲线C上任意一点P(x，y)，由于|PM|－|PN|＝2R－2≤2，

所以R≤2，当且仅当圆P的圆心为(2,0)时，R＝2.

所以当圆P的半径最长时，其方程为(x－2)2＋y2＝4.

若l的倾斜角为90°，则l与y轴重合，可得|AB|＝.

若l的倾斜角不为90°，由r1≠R知l不平行于x轴，设l与x轴的交点为Q，则，可求得Q(－4,0)，所以可设l：y＝k(x＋4)。

由l与圆M相切得＝1，解得k＝.

当k＝时，将代入，并整理得7x2＋8x－8＝0，解得x1,2＝，

所以|AB|＝|x2－x1|＝.

当k＝时，由图形的对称性可知|AB|＝.

综上，|AB|＝或|AB|＝.

知识点

直线的斜截式方程

题型：单选题

单选题 · 5 分

设分别为双曲线的左.右焦点，双曲线上存在点使得则该双曲线的离心率为（）

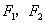
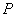
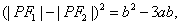
正确答案

解析

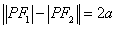
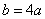
由于，故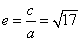，即，分解因式得：

，故，从而，

故，选择

知识点

直线的斜截式方程

题型：填空题

填空题 · 5 分

已知圆的圆心是双曲线的一个焦点，则此双曲线的渐近线方程为。

正确答案

解析

略。

知识点

直线的斜截式方程

题型：填空题

填空题 · 4 分

若函数是定义域为的偶函数，则函数的单调递减区间是　　。

正确答案

解析

略

知识点

直线的斜截式方程

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 直线的两点式方程

百度题库 > 高考 > 文科数学 > 直线的斜截式方程

扫码查看完整答案与解析