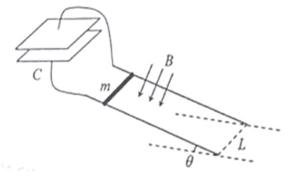
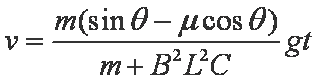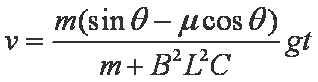- 平行板电容器的电容
- 共18题
如图,一平行板电容器的两个极板竖直放置,在两极板间有一带电小球,小球用一绝缘轻线悬挂于O点,现给电容器缓慢充电,使两极板所带电荷量分别为+Q和-Q,此时悬线与竖直方向的夹角为

正确答案
2Q
解析
设电容器电容为C,第一次充电后两极板之间的电压为
两极板之间电场的场强为

式中d为两极板间的距离。
按题意,当小球偏转角
Tcosθ1=mg③
Tsinθ1=qE④
式中T为此时悬线的张力。
联立①②③④式得

设第二次充电使正极板上增加的电荷量为


联立⑤⑥式得

代入数据解得
知识点
如图,两条平行导轨所在平面与水平地面的夹角为θ,间距为L。导轨上端接有一平行板电容器,电容为C。导轨处于匀强磁场中,磁感应强度大小为B,方向垂直于导轨平面。在导轨上放置一质量为m的金属棒,棒可沿导轨下滑,且在下滑过程中保持与导轨垂直并良好接触。已知金属棒与导轨之间的动摩擦因数为μ,重力加速度大小为g。忽略所有电阻。让金属棒从导轨上端由静止开始下滑,求:
(1)电容器极板上积累的电荷量与金属棒速度大小的关系;
(2)金属棒的速度大小随时间变化的关系。
正确答案
(1)Q=CBLv (2)
解析
(1)设金属棒下滑的速度大小为v,则感应电动势为E=BLv①;
平行板电容器两极板之间的电势差为U=E②;
设此时电容器极板上积累的电荷量为Q,按定义有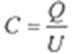
联立①②③式得Q=CBLv④
(2)设金属棒的速度大小为v时经历的时间为t,通过金属棒的电流为I。金属棒受到的电磁场的作用力方向沿导轨向上,大小为f1=BLi④
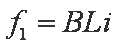
设在时间间隔(t,t+
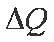
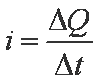


由4式得 
式中,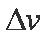
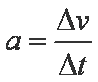
金属棒所受到的摩擦力方向斜向上,大小为
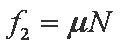
式中,N是金属棒对于轨道的正压力的大小,有
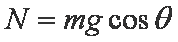
金属棒在时刻t的加速度方向沿斜面向下,设其大小为a,根据牛顿第二定律有
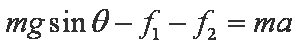
联立5到11式得
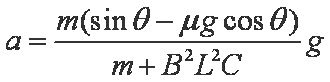
由12式及题设可知,金属棒做初速度为0的匀加速运动。T时刻金属棒的速度大小为
知识点
如图所示电路中,电源电动势为E、内阻为r,电阻R0为定值电阻,R1为滑动变阻器,A、B为电容器的两个极板。当滑动变阻器R1的滑动端处于某位置时,A、B两板间的带电油滴静止不动。则下列说法中正确的是 ( )
正确答案
解析
略
知识点
质量为




求:
(1)飞机模型的起飞距离(离地前的运动距离)以及起飞过程中平均阻力的冲量;
(2)若飞机起飞利用电磁弹射技术,将大大缩短起飞距离。图甲为电磁弹射装置的原理简化示意图,与飞机连接的金属块(图中未画出)可以沿两根相互靠近且平行的导轨滑动。使用前先给电容
①在图乙中画出电源向电容器充电过程中电容器两极板间电压


②当电容器电压为



正确答案
见解析。
解析
(1)平均阻力为f=kmg,依据牛顿第二定律和运动学规律有
F-f=ma
a=
设飞机的起飞距离为s,依据运动学公式
v2=2as
解得s=
设飞机的起飞时间为t
依据运动学公式v=at
平均阻力的冲量I=ft
解得I=
平均阻力冲量的方向与飞机运动方向相反
(2)①见答图2
依据图象可得电容器储存电能的规律
E =
由于q=CU
则电容器充电电压为U0时,
电容器储存电能E0 =

②电容器电压为Um时,电容器储存电能 Em =
设电容器释放的电能为E',由动能定理有
ηE'+Fx-kmgx=
解得E'=
电容器剩余的电能E剩=Em- E'
解得E剩=

知识点
如图,平行板电容器的两个极板与水平地面成一角度,两极板与一直流电源相连。若一带电粒子恰能沿图中所示水平直线通过电容器,则在此过程中,该粒子
正确答案
解析
要使粒子在电场中直线运动,必须使合力与运动方向在一直线上,由题意可受力分析可知,受重力竖直向下,电场力垂直极板向上,合力水平向左。故A错。因电场力做负功,故电势能增加。B正确。合力做负功,故动能减少。C错。因合力为定值且与运动方向在一直线上,故D正确。
知识点
扫码查看完整答案与解析