- 直线与圆、圆与圆的位置关系
- 共336题
本题为选做题,请考生在第22、23、24三题中任选一题做答。如果多做。则按所做的第一题记分.作答时用2B铅笔在答题卡上把所选题目的题号涂黑.。
22.选修4—l:几何证明选讲如图,∠BAC的平分线与BC和△ABC的外接圆分别相交于D和E,延长AC交过D、E、C三点的圆于点F.(Ⅰ)求证:EC=EF;(Ⅱ)若ED=2,EF=3,求AC·AF的值.
23.(本小题满分10分)选修4—4:坐标系与参数方程已知曲线C1的参数方程为


(Ⅰ)求曲线C2的直角坐标方程;(Ⅱ)求曲线C2上的动点M到曲线C1的距离的最大值.
24.(本小题满分10分)选修4—5:不等式选讲 已知函数f(x)=|x-2|-|x+1|.
(Ⅰ)解不等式f(x)>1;(Ⅱ)当x>0时,函数g(x)=
正确答案
22.略.23.(1)



解析
22.试题分析:本题属于平面几何中的基本问题,题目的难度是容易题。
⑴证明:
因为



所以
所以
⑵解:因为

所以

由⑴知,
所以
所以
23.试题分析:本题属于参数方程中的基本问题,题目的难度是容易题。
⑴解:

可得
故

⑵解:

由⑴知曲线



所以动点


24.试题分析:本题属于不等式中的基本问题,题目的难度是容易题。
⑴解:当

当


当


综上,原不等式的解集是
⑵解:因为

所以

所以


考查方向
22.本题考查了平面几何的知识,主要涉及直线与圆的位置关系,三角形相似的考查.
23.本题考查了参数方程的知识,主要涉及直线与圆的位置关系.
24.本题考查了不等式的知识,主要涉及绝对值不等式的解法.
解题思路
22. 1、利用圆的相关定理证明。2、利用切割线定理和相交弦定理证明。
23.本题考查参数方程的知识,解题步骤如下:1、利用公式消参。2、可以利用普通方程求解。
24.本题考查不等式的知识,解题步骤如下:1、利用公式解绝对值不等式。2、可以利用图像求解。
易错点
22.相关的定理容易混用。
23.消参的过程容易出错。
24.去绝对值时容易出错。
知识点
已知函数
(1) 求
(2) 若对于任意的



正确答案
见解析
解析
知识点
抛物线y=
正确答案
解析
抛物线y=
∴
∴准线方程 y=﹣
知识点
设命题p:

正确答案
解析
因为全称命题的否定为特称命题,所以


知识点
某市为了考核甲、乙两部门的工作情况,随机访问了50位市民,根据这50位市民对两部门的评分(评分越高表明市民的评价越高)绘制的茎叶图如图:
(1)分别估计该市的市民对甲、乙两部门评分的中位数;
(2)分别估计该市的市民对甲、乙两部门的评分高于90的概率;
(3)根据茎叶图分析该市的市民对甲、乙两部门的评价。
正确答案
见解析。
解析
(1)由茎叶图知,50位市民对甲部门的评分有小到大顺序,排在排在第25,26位的是75,75,故样本的中 位数是75,所以该市的市民对甲部门的评分的中位数的估计值是75。
50位市民对乙部门的评分有小到大顺序,排在排在第25,26位的是66,68,故样本的中位数是
(2)由茎叶图知,50位市民对甲、乙部门的评分高于90的比率分别为
故该市的市民对甲、乙两部门的评分高于90的概率得估计值分别为0.1,0.16,
(3)由茎叶图知,市民对甲部门的评分的中位数高于乙部门的评分的中位数,而且由茎叶图可以大致看出对甲 部门的评分标准差要小于乙部门的标准差,说明该市市民对甲部门的评价较高、评价较为一致,对乙部门 的评价较低、评价差异较大
知识点
已知函数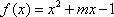
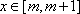
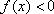
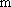
正确答案
解析
二次函数开口向上,在区间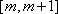
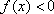
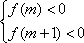
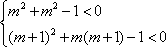
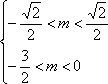
知识点
在平面直角坐标系内,到点A(1,2),B(1,5),C(3,6),D(7,-1)的距离之和最小的点的坐标是__________。
正确答案
(2,4)
解析
由题意可知,若P为平面直角坐标系内任意一点,则
|PA|+|PC|≥|AC|,等号成立的条件是点P在线段AC上;
|PB|+|PD|≥|BD|,等号成立的条件是点P在线段BD上,
所以到A,B,C,D四点的距离之和最小的点为AC与BD的交点。
直线AC方程为2x-y=0,直线BD方程为x+y-6=0,
∴
即所求点的坐标为(2,4)。
知识点
已知a=


正确答案
解析
∵0<a=
b=log2
c=log
∴c>a>b。
知识点
抛物线





正确答案
解析
知识点
4.已知圆



正确答案
解析
易知,圆


考查方向
本题主要考查了两圆的位置关系,在近几年的各省高考题出现的频率较高,常与直线的方程等知识点交汇命题。
解题思路
先分别求出两圆的圆心坐标,再求出圆心距,根据定义判断两圆的位置关系。
易错点
求圆O2的圆心坐标容易出错。
知识点
扫码查看完整答案与解析