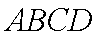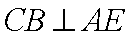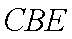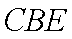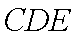- 二次函数的应用
- 共333题
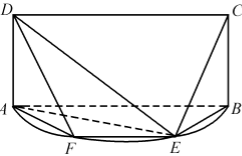
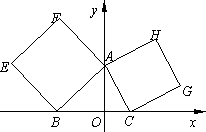
已知集合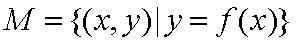
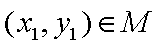
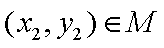
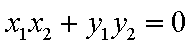
①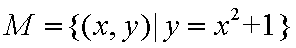
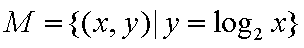
③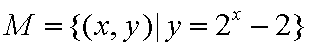
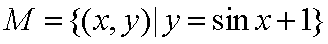
其中是“垂直对点集”的序号是 。
正确答案
答案:
解析
略
知识点
如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F。
(1)若AC-6,AB=10,求⊙O的半径;
(2)连接OE、ED、DF、EF,若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由。
正确答案
见解析。
解析
(1)连接OD。 设⊙O的半径为r。 ∵BC切⊙O于点D,∴OD⊥BC。
∵∠C=90°,∴OD∥AC,∴△OBD∽△ABC。
∴


∴⊙O的半径为
(2)结论:四边形OFDE是菱形。
证明:∵四边形BDEF是平行四边形,
∴∠DEF=∠B。∵∠DEF=∠DOB,∴∠B=∠DOB。
∵∠ODB=90°,∴∠DOB+∠B=90°,∴∠DOB=60°。
∵DE∥AB,∴∠ODE=60°,∵OD=OE,∴△ODE是等边三角形。
∴OD=DE,∵OD=OF,∴DE=OF,∴四边形OFDE是平行四边形。
∵OE=OF,∴平行四边形OFDE是菱形。
知识点
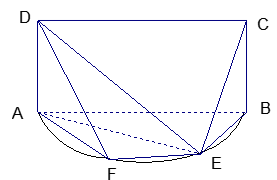
如图,E是以AB为直径的半圆弧上异于A,B的点,矩形ABCD所在平面垂直于该半圆所在的平面,且AB=2AD=2。
(1)求证:EA⊥EC ;
(2)设平面ECD与半圆弧的另一个交点为F,
①求证:EF//AB;
②若EF=1,求三棱锥E—ADF的体积
正确答案
见解析。
解析
(1)∵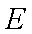
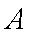
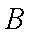
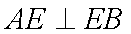
又∵平面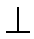
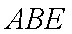
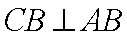
由面面垂直性质定理得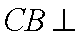
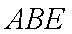
又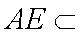
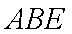
∴
∵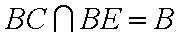
∴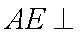
又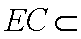
∴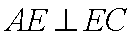
(2) ①由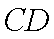
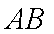
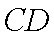
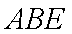
又∵平面
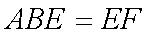
∴根据线面平行的性质定理得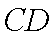
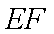
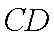
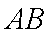
∴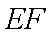
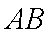
②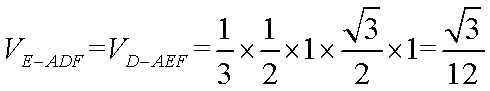
知识点
阅读右面的程序框图,若输出的

正确答案
解析
略
知识点
在平面直角坐标系xOy中,已知点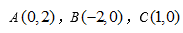
正确答案
解析
略
知识点
扫码查看完整答案与解析