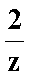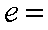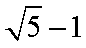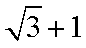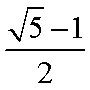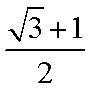- 二次函数的应用
- 共333题
设z=1-i(i是虚数单位),则复数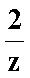
正确答案
解析
因为z=1-i(i是虚数单位),所以复数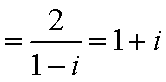
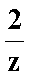
知识点
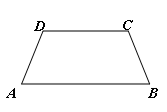
如图,等腰梯形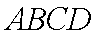
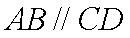
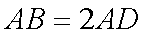
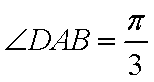
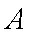
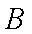
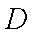
正确答案
解析
由题可知,双曲线离心率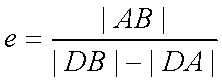
设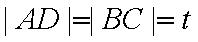
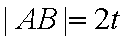
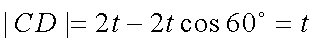
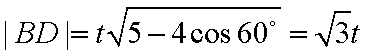
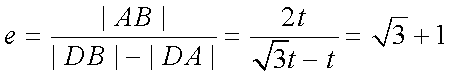
知识点
经市场调查,某城市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数,且销售量近似满足g(t)=80-2t(件),价格近似满足于f(t)= 
(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式;
(2)求该种商品的日销售额y的最大值与最小值。
正确答案
见解析
解析
(1)由已知,由价格乘以销售量可得销售额:
=
(2)由(1)知①当0≤t≤10时y=-t2+10t+1200=-(t-5)2+1225
函数图象开口向下,对称轴为t=5,该函数在t∈[0,5]递增,在t∈(5,10]递减
∴ymax=1225(当t=5时取得),ymin=1200(当t=0或10时取得)
②当10<t≤20时y=t2-90t+2000=(t-45)2-25
图象开口向上,对称轴为t=45,该函数在在t∈(10,20]递减,t=10时,y=1200,ymin=600(当t=20时取得)
由①②知ymax=1225(当t=5时取得),ymin=600(当t=20时取得)
由①②知ymax=1225(当t=5时取得),ymin=600(当t=20时取得)
知识点
已知双曲线

正确答案
解析
略
知识点
已知函数

(1)求
(2)若






正确答案
见解析
解析
(1)


∴


(2)因为

∵





由余弦定理得:
∴
知识点
扫码查看完整答案与解析