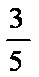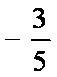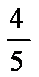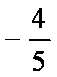- 二次函数的应用
- 共333题
若


正确答案
解析










知识点
某汽车租赁公司为了调查
(1)试根据上面的统计数据,判断这两种车型在本星期内出租天数的方差的大小关系(只需要写出结果);
(2)现
(3)如果两种车型每辆车每天出租得的利润相同,该公司需要购买一辆汽车,请你根据所学的统计知识,给出建议应该购买哪一种车型,并说明你的理由。
正确答案
见解析
解析
解析:(1)由数据的离散程度可以
(2)这辆汽车是A类型车的概率约为
(3)50辆A类型车出租的天数的平均数为
50辆B类型车出租的天数的平均数为
所以应该购买B型车。…………12分
知识点
为了解某校学生的视力情况,现采用随机抽样的方式从该校的A,B两班中各抽5名学生进行视力检测,检测的数据如下:
A班5名学生的视力检测结果:4.3,5.1,4.6,4.1,4.9.
B班5名学生的视力检测结果:5.1,4.9,4.0,4.0,4.5.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?;
(2)由数据判断哪个班的5名学生视力方差较大?(结论不要求证明)
(3)根据数据推断A班全班40名学生中有几名学生的视力大于4.6?
正确答案
见解析
解析
(1)A班5名学生的视力平均数为

(2)B班5名学生视力的方差较大
(3)在A班抽取的5名学生中,视力大于4.6的有2名,所以这5名学生视力大于4.6的频率为

知识点
在





正确答案
解析
由正弦定理得




知识点
某市为了了解市民对卫生管理的满意程度,通过问卷调查了学生、在职人员、退休人员共250人,结果如下表:
若在所调查人员中随机抽取1人,恰好抽到学生的概率为0.32.
(1)求
(2)现用分层抽样的方法在所调查的人员中抽取25人,则在职人员应抽取多少人?
(3)若

(注:
正确答案
见解析
解析
本题主要考查概率、统计等基础知识,考查数据处理能力、抽象概括能力、运算求解能力以及应用意识,考查或然与必然思想、化归与转化思想。
(1)依题意可得
解得
(2)∵学生人数为80,退休人员人数90,
∴在职人员人数为:
可得在职人员应抽取
(3)由

则基本事件

共有9组. ………………9分
由

所以满足条件的基本事件共有7组,………………11分
故所求的概率
知识点
已知数列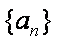
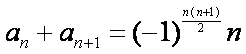
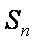
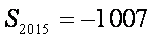
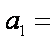
正确答案
解析
略
知识点
已知α∈(,π),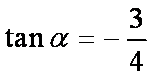
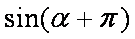
正确答案
解析
由题意可知,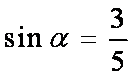
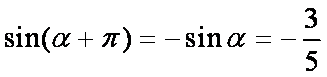
知识点
图是一个几何体的三视图,则该几何体的,表面积为( )
正确答案
解析
由已知中的三视图,我们可以得到该几何体底部是一个底面边长为2的正方体,上部高也为2的四棱锥,
底部分的表面积S1=5×2×2=20,上部分表面积S2=2(

所以表面积为24+4
故选A
知识点
若x1,x2是方程πsin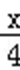
正确答案
4π
解析
函数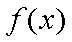
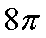
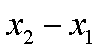
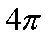
知识点
以直角坐标系的原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线I的参数方程为

(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A ,B两点,当a变化时,求
正确答案
(1)
解析
(1)由



(2)将直线

设A、B两点对应的参数分别为

当
知识点
扫码查看完整答案与解析