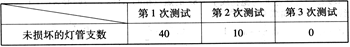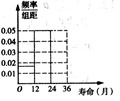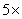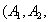- 二次函数的应用
- 共333题
已知以




正确答案
解析
略
知识点
某企业新研制一种LED节能灯管,为了测试其使用寿命,从中随机抽取50支灯管作为测试样本,
分别在使用了12个月、24个月、36个月时进行3次测试,得到未损坏的灯管支数如下表:
(1)请补充完整如图所示的频率分布直方图;
(2)试估计这种节能灯管的平均使用寿命;
(3)某校一间功能室一次性换上5支这种灯管,在使用了12个月时随机取其中3支,求取到已损坏灯管的概率。
正确答案
见解析。
解析
(1)由题意知这种节能灯管的使用寿命在[0,12]上的有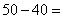
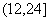
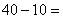
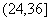
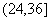
故补充完整的频率分布直方图如图所示,(4分)
(2)取每组的组中值计算灯管的平均使用寿命得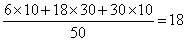
(3)由题易知,S支灯管在使用了12个月时未损坏的有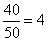
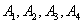
从中随机取3支的所有可能结果有:
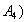
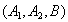
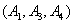
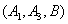
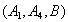
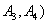
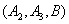
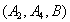
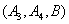
取到已损坏灯管的事件有: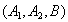
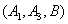
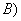
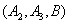
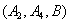
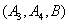
所以取到已损坏灯管的概率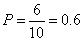
知识点
观察下图2,可推断出“
正确答案
解析
由前两个图形发现:中间数等于四周四个数的平方和,即



知识点
已知变量




正确答案
0.9
解析
略
知识点
在


正确答案
解析
略
知识点
设等比数列




正确答案
解析
略
知识点
设



(1)数表
(2) 数表

(3)对由



正确答案
见解析
解析
(1)
法1:
法2:
法3:
(写出一种即可) …………………3分
(2) 每一列所有数之和分别为2,0,

①如果操作第三列,则
则第一行之和为



② 如果操作第一行
则每一列之和分别为


解得
综上
(3) 证明:按要求对某行(或某列)操作一次时,则该行的行和(或该列的列和)
由负整数变为正整数,都会引起该行的行和(或该列的列和)增大,从而也就使得
数阵中

是改变数表中某行(或某列)各数的符号,而不改变其绝对值,显然,数表中
个数之和必然小于等于
之时必然所有的行和与所有的列和均为非负整数,故结论成立 …………………13分
知识点
某高校组织的自主招生考试,共有1000名同学参加笔试,成绩均介于60分到100分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分为4组:第1组[60,70),第2组[70,80),第3组[80,90),第4组[90,100]。如图是按上述分组方法得到的频率分布直方图,且笔试成绩在85分(含85分)以上的同学有面试资格.
(1)估计所有参加笔试的1000名同学中,有面试资格的人数;
(2)已知某中学有甲、乙两位同学取得面试资格,且甲的笔试比乙的高;面试时,要求每人回答两个问题,假设甲、乙两人对每一个问题答对的概率均为
正确答案
见解析。
解析
(1)设第


所以成绩在85分以上的同学的概率P≈
…………………………………(5分)
故这1000名同学中,取得面试资格的约有1000×0.38=380人.…(6分)
(2)设答对记为1,打错记为0,则所有可能的情况有:
甲00乙00,甲00乙10,甲00乙01,甲00乙11,甲10乙00,甲10乙10,甲10乙01,
甲10乙11,甲01乙00,甲01乙10,甲01乙01,甲01乙11,甲11乙00,甲11乙10,
甲11乙01,甲11乙11,共16个………………………………………(9分)
甲答对题的个数不少于乙的情况有:
甲00乙00,甲10乙00,甲10乙10,甲10乙01,甲01乙00,甲01乙10,甲01乙01,
甲11乙00,甲11乙01,甲11乙10,甲11乙11,共11个……………(11分)
故甲比乙优先获得高考加分资格的概率为
知识点
设


(1)求数列

(2)设数列





正确答案
见解析。
解析
(1)设数列



依题意得:

∵



∴
(2)由题意得
令
则
①-②得:
∴
又
∴
知识点
已知函数
(1)求函数
(2)设


正确答案
见解析。
解析
(1)函数


即
(2)∵

由

∴


∴
知识点
扫码查看完整答案与解析