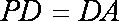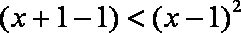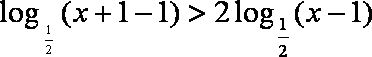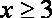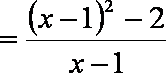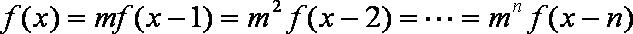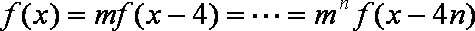- 二次函数的应用
- 共333题
若函数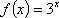
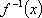
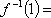
正确答案
0
解析
略
知识点
若圆椎的母线


正确答案
解析
略
知识点
若函数



正确答案
解析
知识点
高三某班学生每周用于数学学习的时间

根据统计资料,该班学生每周用于数学学习的时间的中位数是 ; 根据上表可得回归方程的斜率为3.53,截距为13.5,若某同学每周用于数学学习的时间为18 小时,则可预测该生数学成绩是 分(结果保留整数)。
正确答案
16.5;77
解析
将学习时间重新排列为:24,23,20,19,17,16,16,15,13,11
可得中位数是
当x=18时,
知识点
已知函数







(1)求函数
(2)若锐角


正确答案
(1)
解析
解析:(1)由题意可得





由


函数
(2)由于




知识点
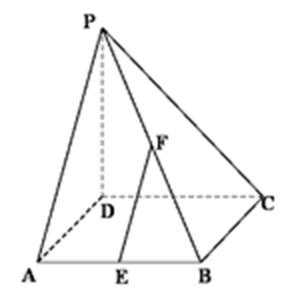
如图,在四棱锥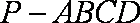
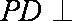
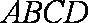
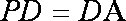
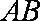
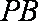
(1)求异面直线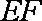
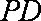
(2)当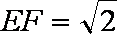
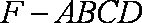
正确答案
见解析
解析
(1)∵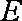
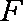
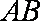
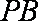
∴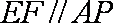
∴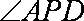
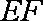
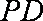
∵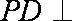
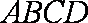
∴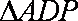
∴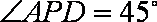
∴异面直线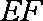
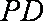
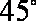
(2)由(1)知,
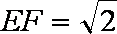
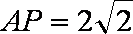
又由题意知,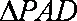
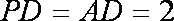
又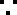
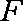
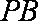
知识点
已知函数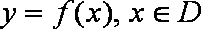
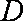
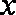
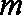
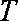
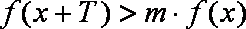
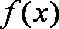
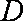
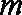
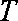
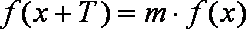
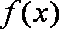
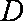
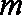
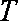
(1)试判断函数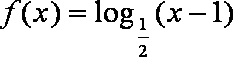
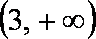
(2)已知函数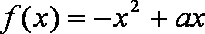
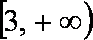
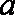
(3)下面两个问题可以任选一个问题作答,问题(Ⅰ)6分,问题(Ⅱ)8分,如果你选做了两个,我们将按照问题(Ⅰ)给你记分。
(Ⅰ)已知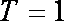
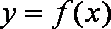
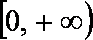
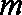
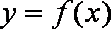
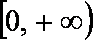
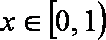
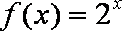
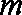
(Ⅱ)已知当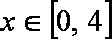
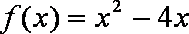
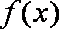
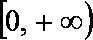
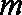
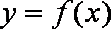

正确答案
见解析
解析
(1)∵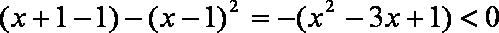
∴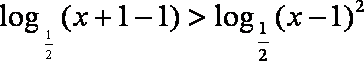
即 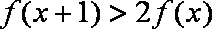
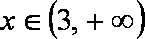
故 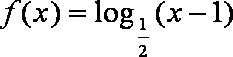
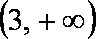
(2)由题意可知: 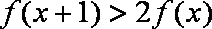
即 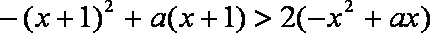
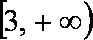
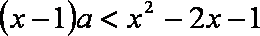
∵
∴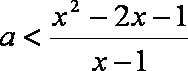
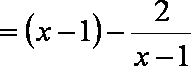
令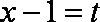
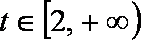
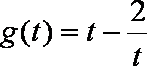
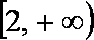
所以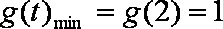
所以
(3)问题(Ⅰ)∵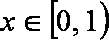
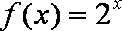
∴当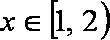
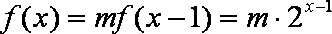
当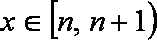
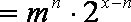
即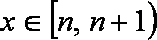
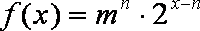
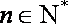
∵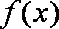
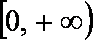
∴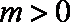
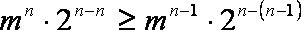
即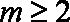
问题(Ⅱ):∵当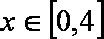
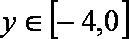
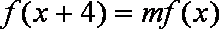
∴当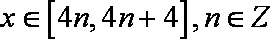
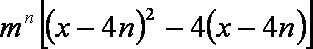
当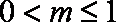
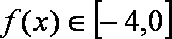
当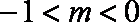

当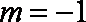
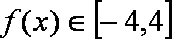
当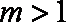
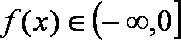
当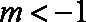
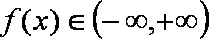
综上可知: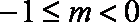
知识点
已知函数
(1)求函数
(2)若直线



(3)设函数




正确答案
见解析。
解析
(1)
而










所以

(2)设切点坐标为

所以切线
又切线

解得


(3)











当





当1<





当



所以

综上,当



当

知识点
已知






正确答案
见解析
解析



由

由

∴当

当

知识点
若直线


正确答案
解析
略
知识点
扫码查看完整答案与解析