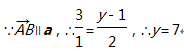- 二次函数的应用
- 共333题
已知函数

(1)求
(2)求
正确答案
见解析
解析
(1)令

所以

由 


由 


综上,函数


(2)
因为

当



当



知识点
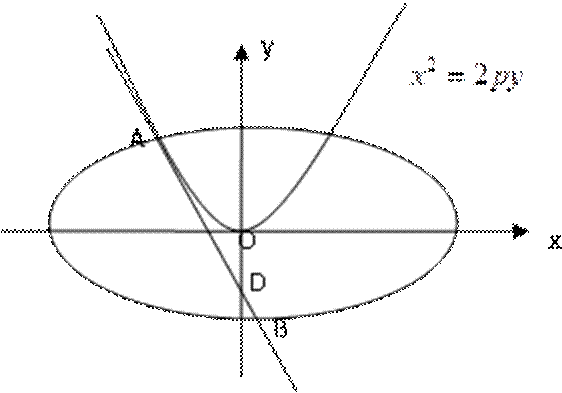
已知向量

(1)若

(2)若


正确答案
见解析。
解析
(1)由


所以
(2)由

即
又


所以
知识点
如图,设













(1)证明:

(2)证明:平面

正确答案
见解析
解析
(1)在折起后的图中,取




∵



∴

又∵



∴

∴四边形
∴
又∵



∴

(2) 在折起后的图中,∵

∴



∴
∵


又∵



∵

∵




∵

∵


∵



知识点
已知点
正确答案
解析
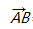
知识点
已知

(1)求
(2)若
(3)证明:
正确答案
见解析
解析
(1)


(2)由(1)知,
令
则

①当

若






②






所以
综上所述,所求的取值范围是
(3)有(2)知当


取
令


即
所以
上式中n=1,2,3,…,n,然后n个不等式相加得到
知识点
如图,已知点D(0,-2),过点D作抛物线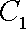
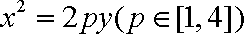
(1)求切点A的纵坐标;
(2)若离心率为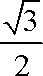
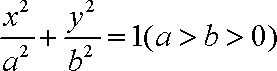
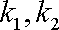
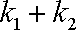
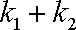
正确答案
见解析。
解析
解析:(1)设切点A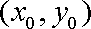
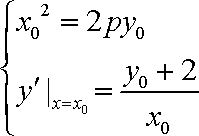
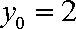
(2)依题意可设椭圆的方程为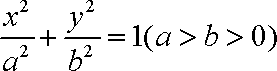
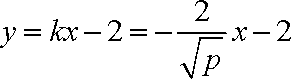
由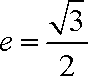
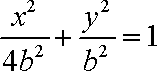
由(1)可得A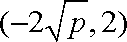
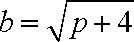
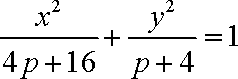
联立直线AB与椭圆的方程: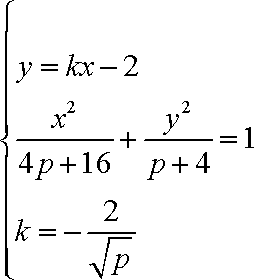
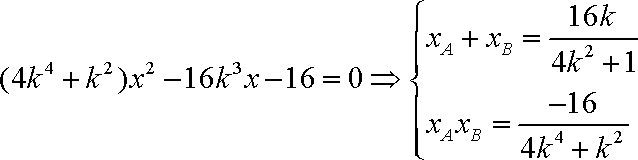
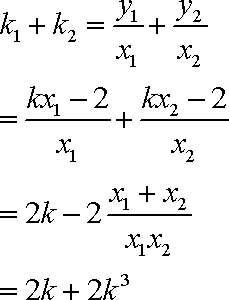
又∵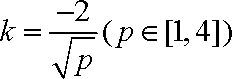
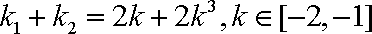
(3)由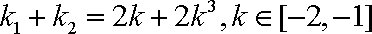
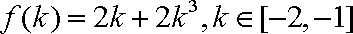
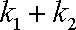
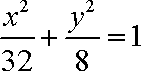
知识点
已知函数
(1)设P,Q是函数
(2)求实数


正确答案
见解析
解析
解:(1)由题意,得
所以函数
设



(2)当

当


①当


所以

所以
②当


于是
因为


所以

所以

亦即
(i)当


所以


(ii)当


当



从而

综上所述,实数

知识点
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分,现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形


(1)求V关于θ的函数表达式;
(2)求
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由。
正确答案
见解析。
解析
(1)梯形



体积
(2)
令


∵

当


当


∴当
(3)木梁的侧面积





设


∴当


又由(2)知

所以
综上,当木梁的体积V最大时,其表面积S也最大。
知识点
设函数
(1)求
(2)在锐角△







正确答案
见解析。
解析
(1)
=
所以

值域为
(2)由





∵


在△ABC中,由正弦定理得
∴
知识点
设函数f(x)=log2x(0<x<5),则f(x)<1的概率为 。
正确答案
解析
∵函数f(x)=log2x(0<x<5),f(x)<1,
∴log2x<1,解得0<x<2,
根据几何概型的概率公式可得,
若从区间(0,5)内随机选取一个实数x,f(x)<1的概率为:P=

知识点
扫码查看完整答案与解析