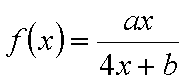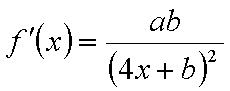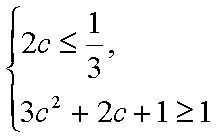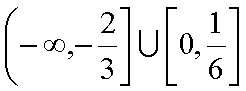- 二次函数的应用
- 共333题
已知函数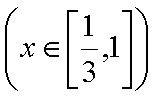

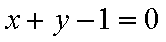
(1)求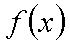
(2)设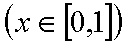
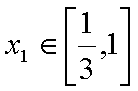
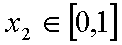
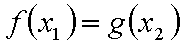

正确答案
见解析
解析
(1)将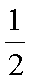
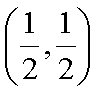
所以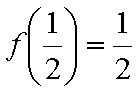
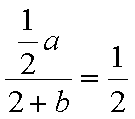
由导数的几何意义得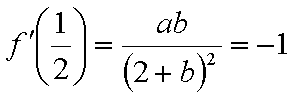
联立①②,解之得:
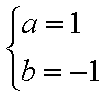
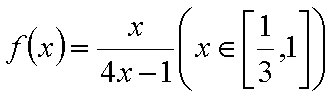
(2)由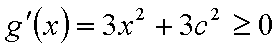
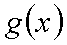
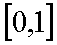
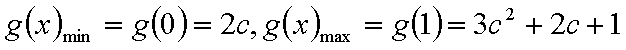
故函数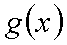
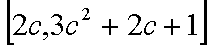
因为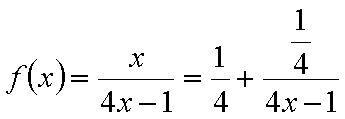
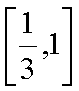
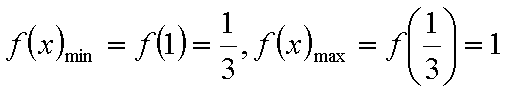
故函数
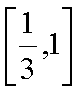
由题设得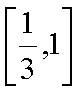
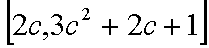
则
解得
知识点
已知正项数列



(1)证明数列
(2)若


正确答案
见解析
解析
(1)证明:由题意知
当

当
两式相减得


由于



即数列

∴数列

(2)由(1)知



知识点
若a>b>0,则下列不等式不成立的是 ( )
正确答案
解析
由不等式的性质知
知识点
已知椭圆




(1)求椭圆
(2)设直线









正确答案
见解析。
解析
(1)依题意,
从而
点

解得

椭圆

(2)由


由椭圆的对称性知,
由


所以直线

即
由
得

所以直线






知识点
已知函数
(1)求函数
(2)在




正确答案
见解析
解析
(1)


由


故


(2)
又

知识点
扫码查看完整答案与解析