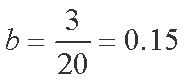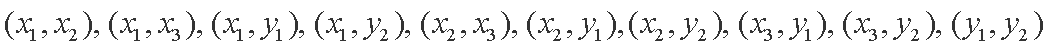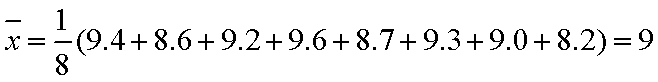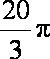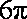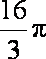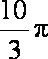- 二次函数的应用
- 共333题
某种产品按质量标准分成五个等级,等级编号依次为1,2,3,4,5,现从一批产品中随机抽取20件,对其等级编号进行统计分析,得到频率分布表如下:
(1)若所抽取的20件产品中,等级编号为4的恰有3件,等级编号为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级编号为4的3件产品记为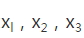
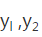
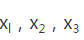
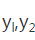
正确答案
(1)a=0.1,b=0.15,c=0.1(2)P(A)=0.4
解析
解析:(1)由频率分布表得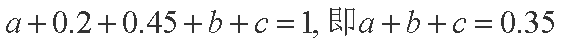
因为抽取的20件产品中,等级编号为4的恰有3件,所以
等级编号为5的恰有2件,所以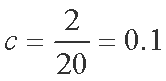
从而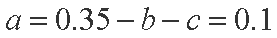
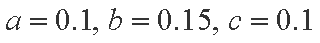
(2)从产品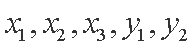
共10种 …………………………………………………………………………………8分
设事件A表示“从产品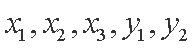
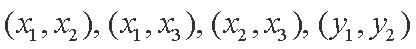
故所求的概率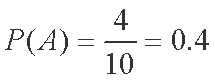
知识点
如图,AB、CD是⊙O的两条平行切线,B、D为切点,AC为
⊙O的切线,切点为E,过A作AF⊥CD,F为垂足。
(1)求证:四边形ABDF是矩形;
(2)若AB=4,CD=9,求⊙O的半径。
正确答案
见解析
解析
解析:(1)连结OB,并作BO的延长线,
∵AB切⊙O于B,∴OB⊥AB
∵AB∥CD,∴BO⊥CD,∴BO经过D点
∴BD为⊙O直径
又∵AF⊥CD,∴四边形ABDF是矩形………………5分
(2)在RtΔACF中,
由切线长定理得 AB=AE, CE=CD
∴AC=AE+CE=AB+CD=13,CF=CD-DF=CD-AB=5
∴AF=
即⊙O的半径长为6………………………………………………………………………10分
知识点
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位:辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆。
(1)求z的值;
(2)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下: 9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2. 把这8辆轿车的得分看作一个总体,从中任取一个分数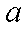
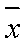
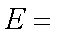
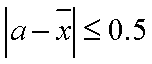
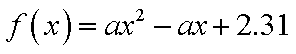
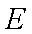
正确答案
见解析。
解析
(1)设该厂本月生产轿车为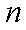
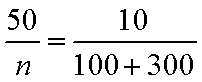
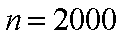
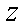
(2) 8辆轿车的得分的平均数为
…………………………………………6分
把8辆轿车的得分看作一个总体,从中任取一个分数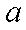
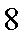
由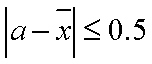
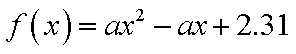
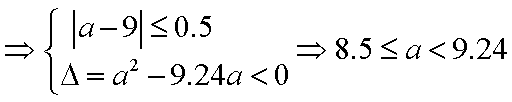
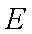
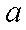
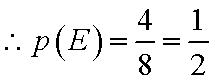
知识点
在△ABC中,角A,B,C所对的边分别为a,b,c,且
(1)求
(2)若
正确答案
见解析。
解析
(1)

(2)∵在











知识点
已知函数
(1)求f(x)的最小正周期;
(2)求f(x)在区间
正确答案
见解析。
解析
(1)化简可得
=
=
=
所以
(2)因为
所以
当

当

知识点
若向量




(1) 求
(2) 当

正确答案
见解析。
解析
(1)∵周期为

又∵
∴


∴
(2)∵



由

所以a的取值范围为
知识点
设函数

(1)求
(2)若






正确答案
见解析。
解析
(1)




当


当


(2)因为
即
∴
∵


∴

由余弦定理得:
∴
知识点
设

(1)当
(2)当
正确答案
见解析。
解析
(1)
由正弦定理得




由余弦定理
得4=

∴
∴
知识点
已知⊙O1和⊙O2的极坐标方程分别是



(1)将两圆的极坐标方程化为直角坐标方程;
(2)若两圆的圆心距为
正确答案
(1)
解析
解析:(1)由
所以⊙O1的直角坐标方程为
所以⊙O2的直角坐标方程为
(2)⊙O1与⊙O2的圆心距为

知识点
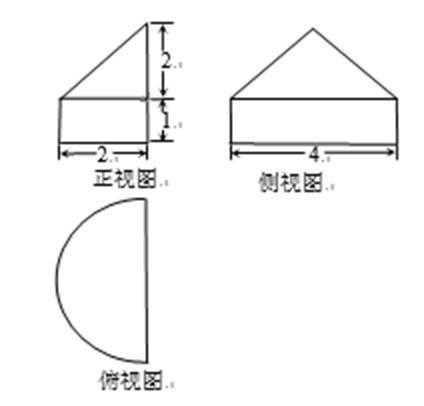
某几何体的三视图如图所示,则此几何体的体积是
正确答案
解析
此几何体为半个圆锥与半个圆柱的组合体,体积
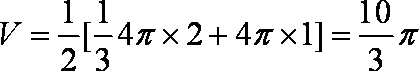
知识点
扫码查看完整答案与解析