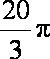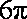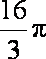- 二次函数的应用
- 共333题
已知函数
(1)求f(x)的最小正周期;
(2)求f(x)在区间
正确答案
见解析。
解析
(1)化简可得
=
=
=
所以
(2)因为
所以
当

当

知识点
若向量




(1) 求
(2) 当

正确答案
见解析。
解析
(1)∵周期为

又∵
∴


∴
(2)∵



由

所以a的取值范围为
知识点
设函数

(1)求
(2)若






正确答案
见解析。
解析
(1)




当


当


(2)因为
即
∴
∵


∴

由余弦定理得:
∴
知识点
设

(1)当
(2)当
正确答案
见解析。
解析
(1)
由正弦定理得




由余弦定理
得4=

∴
∴
知识点
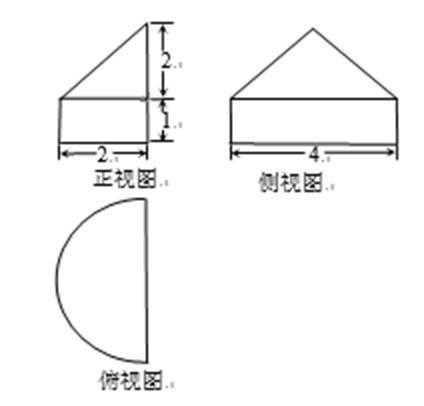
某几何体的三视图如图所示,则此几何体的体积是
正确答案
解析
此几何体为半个圆锥与半个圆柱的组合体,体积
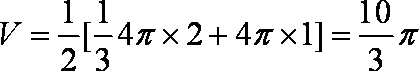
知识点
扫码查看完整答案与解析