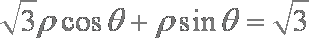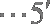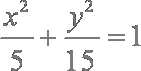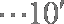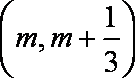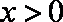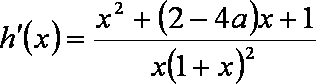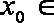- 二次函数的应用
- 共333题
在直角坐标系中,曲线C的参数方程为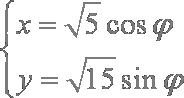
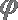
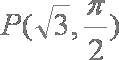

(1)判断点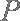
(2)设直线l与曲线C的两个交点为A、B,求
正确答案
见解析
解析
(1)直线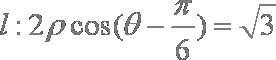


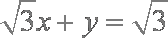

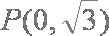
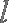
(2)直线
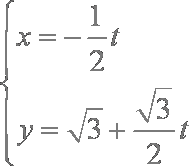
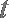
曲线C的直角坐标方程为
将直线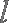
有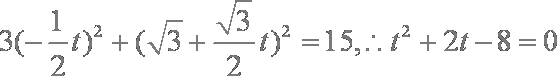
设两根为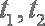
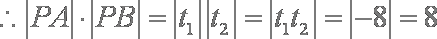
知识点
如图,






(1)求证:平面
(2)求几何体ABCDEF的体积
正确答案
见解析
解析
(1)

又

(2)因为










所以几何体的体积
知识点
已知


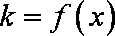
(1)若函数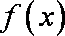

(2)设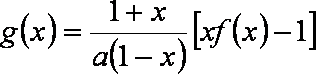
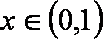
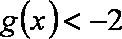

正确答案
见解析
解析
(1)由题意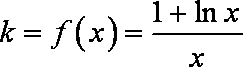
所以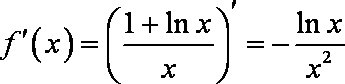
当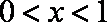


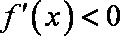


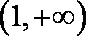
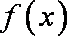
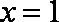
因为函数

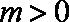
所以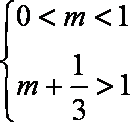
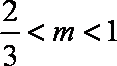


(2)由题可知,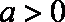
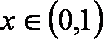

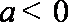
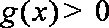
当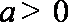
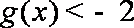


设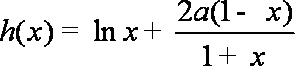
设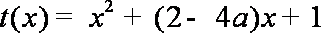
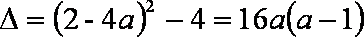
①若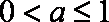
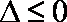

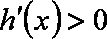
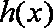
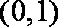
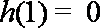

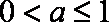
②若

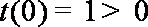


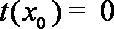
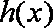
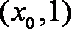
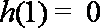
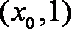
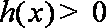
综合①②可得
知识点
抛物线y2 = 8x的焦点到双曲线 – = 1的渐近线的距离为___▲__。
正确答案
1
解析
由题意有,抛物线y2 = 8x的焦点为(2,0),双曲线的渐近线方程中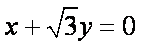
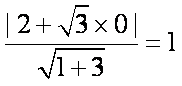
知识点
已知数列



(1)求数列
(2)设



正确答案
见解析
解析
(1) 当


当
∴


故

(2)由(1)知



故使


知识点
扫码查看完整答案与解析