- 偶函数
- 共20题
7.已知定义在R上的函数
A
B
C
D
正确答案
解析
由
考查方向
解题思路
函数是高考中的重点与热点,客观题中也会出现较难的题,解决此类问题要充分利用相关结论.函数
易错点
函数单调性的正确运用
知识点
3.下列函数
A
B
C
D
正确答案
解析
根据题意可知，A B为偶函数，对于A选项，函数在
考查方向
解题思路
先找出偶函数，再找到增函数
易错点
对函数的性质掌握不好
知识点
8.已知函数
A
B
C
D
正确答案
解析
由已知，f(x)在
考查方向
偶函数的性质
函数的增减性
解题思路
先求出a.b.c的值，然后判断大小
易错点
根据指数的运算性质和对数的运算性质计算
知识点
已知函数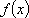
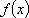
正确答案
解析
由f(x＋2)＝f(x)知f(x)是周期为2的函数，
∴f(-2011)＋f(2012)＝f(2011)＋f(2012)＝f(1)＋f(0)＝log22＋log21＝1.
知识点
设{
（1）求数列{
（2）设
正确答案
见解析。
解析
解：（1）由已知，得
解得
设数列
∴
∴
(2)∵
∴
知识点
f(x)为偶函数且
正确答案
4
解析
依题意， 
知识点
已知
A
B
C
D
正确答案
解析
略
知识点
已知
（1）求实数
（2）若关于
正确答案
见解析
解析
（1）由函数
（2）由
知识点
命题“若a，b都是偶数，则a+b是偶数”的否命题是 若a，b不都是偶数，则a+b不是偶数 。
正确答案
若a，b不都是偶数，则a+b不是偶数。
解析
解：条件和结论同时进行否定，则否命题为：若a，b不都是偶数，则a+b不是偶数。
知识点
己知函数f（x+1）是偶函数，当x∈（1，+∞）时，函数f（x）单调递减，设a=f（﹣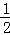
正确答案
解析
∵函数f（x+1）是偶函数，当x∈（1，+∞）时，函数f（x）单调递减，
∴当x∈（﹣∞，1）时，函数f（x）单调递增，
∵b=f（3）=f（﹣1），﹣1＜﹣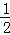
∴f（﹣1）＜f（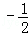
∴f（3）＜f（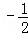
∴b＜a＜c
故选A。
知识点
扫码查看完整答案与解析