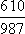算法初步_章节学习

1

题型：单选题

|

单选题 · 5 分

9.执行右面的程序框图,如果输入的,则输出x,y的值满足

A

B

C

D

正确答案

C

解析

试题分析：当时，，不满足；，不满足；，满足；输出，则输出的的值满足，故选C.

考查方向

本题主要考查了程序框图与算法案例，在近几年的各省高考题出现的频率较高，常与数列、函数等知识点交汇命题。

解题思路

求解此类问题一般是把人看作计算机,按照程序逐步列出运行结果。

易错点

不知何时终止循环导致出错。

知识点

选择结构

1

题型：单选题

|

单选题 · 5 分

8.中国古代有计算多项式值的秦九韶算法，下图是实现该算法的程序框图.执行该程序框图，若输入的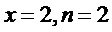，依次输入的为2，2，5，则输出的（）

A7

B12

C17

D34

正确答案

C

解析

C

第一次运算：，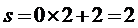

第二次运算：，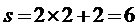

第三次运算：，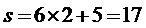

故选C．

考查方向

本题主要考查了程序框图，直到型循环结构，在近几年的各省高考题出现的频率较高，常与数列、函数等知识点交汇命题。

解题思路

求解此类问题一般是把人看作计算机,按照程序逐步列出运行结果。

易错点

不知何时终止循环导致出错。

知识点

选择结构

1

题型：填空题

|

填空题 · 4 分

（4分）（2015•上海）若线性方程组的增广矩阵为解为，则c1﹣c2=　　　　　　．

正确答案

16

知识点

选择结构

1

题型：单选题

|

单选题 · 5 分

3.执行如图所示的程序框图，若输入的a值为1，则输出的k值为( )

A1

B2

C3

D4

正确答案

B

知识点

选择结构

1

题型：填空题

|

填空题 · 5 分

6.如图是一个算法的流程图，则输出的值是．

正确答案

9；

解析

的变化如下表：

则输出时．

考查方向

循环结构流程图

解题思路

根据算法的程序流程逐项验证，直到循环终止输出结果。

易错点

循环终止的条件

知识点

选择结构

1

题型：单选题

|

单选题 · 5 分

6.执行如图所示的程序框图，则输出的实数m的值为（）

A9

B10

C11

D12

正确答案

C

解析

M=1 T=1,T<99,T=1,M=2;

M=2,T=1,T<99,T=4,M=3;

M=3,T=4,T<99.T=9,M=4;

…………

M=10,T=81,T<99,T=100,M=11;

M=11,T=100,T>99,输出m,所以m=11.故选C

考查方向

流程图

解题思路

顺序结构循环结构判断结构

易错点

循环语句理解错误，判断条件看错

知识点

选择结构

1

题型：填空题

|

填空题 · 5 分

13．执行如图程序框图，输出的T的值为　　．

正确答案

解析

模拟执行程序框图，可得n=1，T=1

满足条件n＜3，T=1+xdx，n=2

满足条件n＜3，T=1+xdx+x2dx=1+，n=3

不满足条件n＜3，退出循环，输出T的值为．

故答案为：.

考查方向

本题主要考查了循环结构的程序框图，考查了定积分的应用，属于基本知识的考查．

解题思路

模拟执行程序框图，依次写出每次循环得到的n，T的值，当n=3时不满足条件n＜3，退出循环，输出T的值为．

易错点

知识点

选择结构

1

题型：单选题

|

单选题 · 5 分

4．如图所示，程序框图输出的所有实数对所对应的点都在函数（）

A的图象上

B的图象上

C的图象上

D的图象上

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

选择结构

1

题型：填空题

|

填空题 · 5 分

11.执行右边的程序框图，若输入的a,b的值分别为0和9，则输出的i的值为________.

正确答案

3

解析

第一次循环：a=1，b=8；第二次循环：a=3，b=6；第三次循环：a=6，b=3；满足条件，结束循环，此时，i=3.

考查方向

本题考查循环结构框图，推理与归纳能力，难度较低。

解题思路

根据循环结构逐一运算,直到满足输出条件终止循环,输出结果.

易错点

循环的终止条件和控制循环变量求解

知识点

选择结构

1

题型：单选题

|

单选题 · 5 分

7．执行如图的程序框图（）,则输出的S=

A

B

C

D

正确答案

C

解析

执行第一次循环体运算，得；

执行第二次，；

执行第次，，故选.

考查方向

本题主要考查学生对程序框图的认识与理解以及等比数列求和公式的应用,意在考查考生对基础知识的掌握程度和运算求解能力。本处在近几年的各省高考题出现的频率较高，常与三角求值，函数求值、数列求和等知识点交汇命题。

解题思路

分条件不断赋值得到S

易错点

1、本题易在由框图认知项的个数上出错。

2、本题极易忽视等比数列求和公式中取1这种情况而选错求和公式。

知识点

选择结构

1

题型：单选题

|

单选题 · 5 分

8.执行下面的程序框图，则输出的的值为（）

A10

B11

C1024

D2048

正确答案

C

解析

利用列表的形式即可解得：

考查方向

本题考查了程序框图中的循环结构，和等比数列的前n项和的概念。

解题思路

由循环结构的特点，先判断，再执行，分别计算出当前的n，S的值，即可得到结论。

易错点

最后运行的次数。

知识点

选择结构

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：单选题

|

单选题 · 5 分

执行如图所示的程序框图，输出的S值为(　　)。

A1

B

C

D

正确答案

C

解析

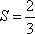
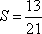
依次执行的循环为S＝1，i＝0；，i＝1；，i＝2.故选C.

知识点

循环结构程序框图

1

题型：简答题

|

简答题 · 13 分

已知双曲线E：﹣=1（a＞0，b＞0）的两条渐近线分别为l1：y=2x，l2：y=﹣2x。

（1）求双曲线E的离心率；

（2）如图，O为坐标原点，动直线l分别交直线l1，l2于A，B两点（A，B分别在第一、第四象限），且△OAB的面积恒为8，试探究：是否存在总与直线l有且只有一个公共点的双曲线E？若存在，求出双曲线E的方程，若不存在，说明理由。

正确答案

（1）因为双曲线E的渐近线分别为l1：y=2x，l2：y=﹣2x，

所以=2。

故c=a，

从而双曲线E的离心率e==。

（2）由（1）知，双曲线E的方程为﹣=1。

设直线l与x轴相交于点C，

当l⊥x轴时，若直线l与双曲线E有且只有一个公共点，则|OC|=a，|AB|=8，

所以|OC|•|AB|=8，

因此a•4a=8，解得a=2，此时双曲线E的方程为﹣=1。

以下证明：当直线l不与x轴垂直时，双曲线双曲线E的方程为﹣=1也满足条件。

设直线l的方程为y=kx+m，依题意，得k＞2或k＜﹣2；

则C（﹣，0），记A（x1，y1），B（x2，y2），

由得y1=，同理得y2=，

由S△OAB=|OC|•|y1﹣y2|得：

|﹣|•|﹣|=8，即m2=4|4﹣k2|=4（k2﹣4）。

因为4﹣k2＜0，

所以△=4k2m2+4（4﹣k2）（m2+16）=﹣16（4k2﹣m2﹣16），

又因为m2=4（k2﹣4），

所以△=0，即直线l与双曲线E有且只有一个公共点。

因此，存在总与直线l有且只有一个公共点的双曲线E，且E的方程为﹣=1。

解析

压轴题；圆锥曲线的定义、性质与方程。

（1）依题意，可知=2，易知c=a，从而可求双曲线E的离心率；

（2）由（1）知，双曲线E的方程为﹣=1，设直线l与x轴相交于点C，分l⊥x轴与直线l不与x轴垂直讨论，当l⊥x轴时，易求双曲线E的方程为﹣=1.当直线l不与x轴垂直时，设直线l的方程为y=kx+m，与双曲线E的方程联立，利用由S△OAB=|OC|•|y1﹣y2|=8可证得：双曲线E的方程为﹣=1，从而可得答案。

知识点

循环结构

1

题型：单选题

|

单选题 · 5 分

当时，执行如图所示的程序框图，输出的值为（）

A7

B42

C210

D840

正确答案

C

解析

知识点

循环结构程序框图

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点