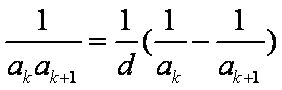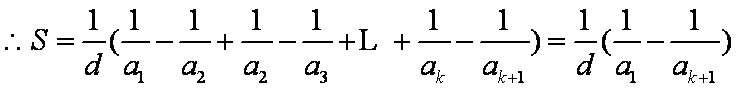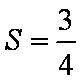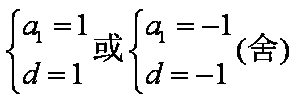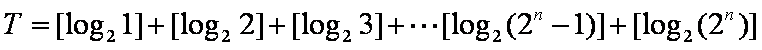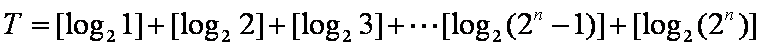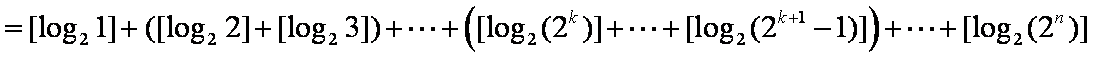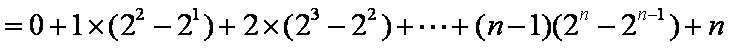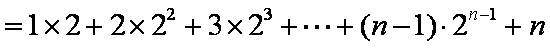- 设计程序框图解决实际问题
- 共59题
如图,是一程序框图,则输出结果为K= ,S= 。
(说明,M=N是赋值语句,也可以写成M←N,或M:=N)
正确答案
11,
解析
知识点
下图是某算法的程序框图,则程序运行后输出的结果是 .
正确答案
27
解析
由框图的顺序,s=0,n=1,s=(s+n)n=(0+1)*1=1,n=n+1=2,依次循环
s=(1+2)*2=6,n=3,注意此刻3>3仍然是否,所以还要循环一次s =(6+3)*3=27,n=4,
此刻输出s=27.
知识点
为调查某市中学生平均每人每天参加体育锻炼时间X(单位:分钟),按锻炼时间分下列4种情况统计:
①0~10分钟;②11~20分钟;③21~30分钟;④30分钟以上.有10000名中学生参加了此项调查活动,右图是此次调查中某一项的流程图,其输出的结果是6200.则平均每天参加体育锻炼时间在0~20分钟内的学生的频率是
正确答案
解析
由流程图可知输出的

知识点
执行右边的程序框图,则输出的a值是 。
正确答案
121
解析
略
知识点
某省高考数学阅卷点共有400名阅卷老师,为了高效地完成文、理科数学卷的阅卷任务,需将400名阅卷老师分成两组同时展开阅卷工作,一组完成269捆文科卷,另一组完成475捆理科卷,根据历年阅卷经验,文科每捆卷需要一位阅卷老师工作3天完成,理科每捆卷需要一位阅卷老师工作4天完成,(假定每位阅卷老师工作一天的阅卷量相同,每捆卷的份数也相同)
(1)如何安排文、理科阅卷老师的人数,使得全省数学阅卷时间最省?
(2)由于今年理科阅卷任务较重,理科实际每捆卷需要一位阅卷老师工作4.5天完成,在按(1)分配的人数阅卷4天后,阅卷领导小组决定从文科组抽调20名阅卷老师去阅理科卷,试问完成全省数学阅卷任务至少需要多少天?(天数精确到小数点后第3位)
(参考数据:



正确答案
见解析
解析
(1)设文科阅卷人数为

则阅卷时间为
而

答:当文、理科阅卷人数分别是119,281时,全省阅卷时间最省;
(2)文科阅卷时间为:
理科阅卷时间为:
答:全省阅卷时间最短为
知识点
某程序的框图如图所示,若输出的结果不大于37,则输入的整数
正确答案
5
解析
由S=0,n=0得出S=0+20+1=2,n=1;
由S=2,n=1得出S=2+21+1=5,n=2;
由S=5,n=2得出S=5+22+1=10,n=3;
由S=10,n=3得出S=10+23+1=19,n=4;
由S=19,n=4得出S=19+24+1=36<37,n=5;
由S=36,n=5得出S=36+25+1>37,
∴当S=36时为满足条件时输出的结果,应终止循环,
因此判定输入的整数i的最大值为5。
知识点
按下列程序框图来计算,若输入x=10,则运算的次数为
正确答案
解析
第一次循环,x=3x-2=28,不满足条件x>2014,再次循环;
第二次循环,x=3x-2=82,不满足条件x>2014,再次循环;
第三次循环,x=3x-2=244,不满足条件x>2014,再次循环;
第四次循环,x=3x-2=730,不满足条件x>2014,再次循环;
第五次循环,x=3x-2=2188,满足条件x>2014,结束循环,
因此循环次数为5次。
知识点
执行如右图的程序框图,若输出的

正确答案
解析
略
知识点
如图,

正确答案
解析
打印出的第5组数据是学号为8号,且成绩为361,故结果是
知识点
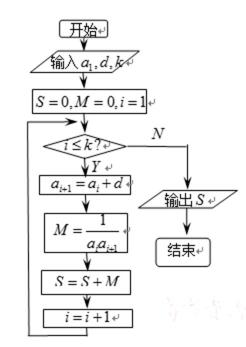
已知数列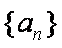
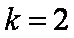
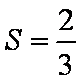
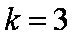
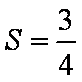
(1)试求数列
(2)设若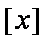
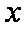
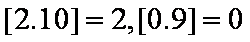
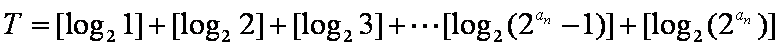
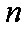
正确答案
见解析
解析
由框图可知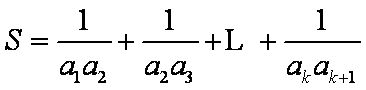
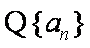

(1)由题意知若
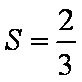
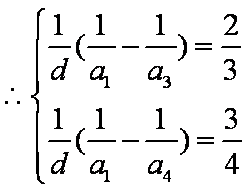
故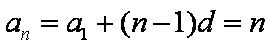
(2)由题意可设
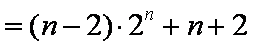
知识点
扫码查看完整答案与解析