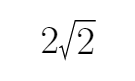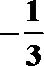- 运用诱导公式化简求值
- 共45题
1
题型:简答题
|
已知函数
(1)若函数
(2)令


(3)当
正确答案
见解析
解析
解析:(1)
令


所以
(2)假设存在实数a,使

①当

②当


所以
③当

综上,存在实数

(3)令



当



所以
所以

知识点
运用诱导公式化简求值
1
题型:填空题
|
已知数列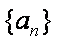

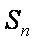
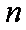
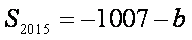
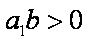
则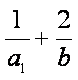
正确答案
3+
解析
略
知识点
运用诱导公式化简求值
1
题型:
单选题
|
5.已知函数

正确答案
A
解析
解析已在路上飞奔,马上就到!
知识点
运用诱导公式化简求值
1
题型:填空题
|
10. 已知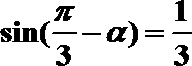
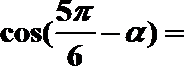
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
运用诱导公式化简求值
1
题型:
单选题
|
1. 
正确答案
A
解析
解析已在路上飞奔,马上就到!
知识点
三角函数的化简求值运用诱导公式化简求值
下一知识点 : 两角和与差的余弦函数
扫码查看完整答案与解析