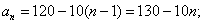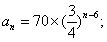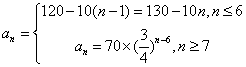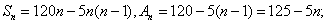- 函数模型及其综合应用
- 共61题
8.某食品的保鲜时间









正确答案
考查方向
易错点
1.没有发现192与48之间的关系导致不会解方程组;
知识点
21.已知一企业生产某产品的年固定成本为10万元,每生产千件需另投入2.7万元,设该企业年内共生产此种产品

(1)写出年利润

(2)年产量为多少千件时,该企业生产此产品所获年利润最大?(注:年利润=年销售收入-年总成本)
正确答案
(1)当

当

(2)①当




当





②当

当且仅当


综合①、②知

所以为9千件时,该企业生产此产品获利最大.
解析
解析已在路上飞奔,马上就到!
知识点
17.即将开工的上海与周边城市的城际列车铁路线将大大缓解交通的压力,加速城市之间的流通。根据测算,如果一列火车每次拖4节车厢,每天能来回16次;如果每次拖7节车厢,则每天能来回10次。每天来回次数是每次拖挂车厢个数的一次函数,每节车厢一次能载客110人,试问每次应拖挂多少节车厢才能使每天营运人数最多?并求出每天最多的营运人数。(注:营运人数指火车运送的人数)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某通讯公司需要在三角形地带









设


(1)试将


(2)当

正确答案
(1)



解析
(1)结合图形可知,
于是,
解得
(2)由(1)知,
因此,



答:当


知识点
对任意实数a,b定义运算“



正确答案
解析
略
知识点
已知函数



(1)求
(2)若


正确答案
见解析。
解析
解:(1)由

又∵

∴
(2)由

∵


∴
知识点
已知


正确答案
解析
略
知识点
某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少,从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%。
(1)求第n年初M的价值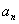
(2)设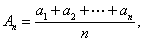
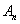
正确答案
见解析
解析
(1)当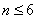
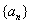
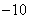
当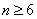
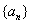
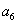
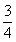
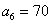
因此,第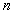
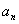
(2)设
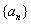
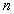
当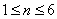
当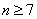
因为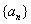
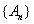
所以须在第9年初对M更新。
知识点
某城市随机抽取一个月(30天)的空气质量指数
(1)根据以上数据估计该城市这30天空气质量指数
(2)若该城市某企业因空气污染每天造成的经济损失


若在本月30天中随机抽取一天,试估计该天经济损失
正确答案
(1)175(2)
解析
解析:(1)该城市这30天空气质量指数

(2)设“在本月30天中随机抽取一天,该天经济损失
由

根据表格数据得共有9+4=13天
所以 
知识点
扫码查看完整答案与解析