函数模型及其综合应用_章节学习

1

题型：填空题

|

填空题 · 5 分

16．对于实数a，b，定义运算“⊗”：a⊗b=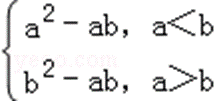，设f（x）=（2x﹣1）⊗（x﹣1），且关于x的方程f（x）﹣m=0恰有三个互不相等的实数根，则实数m的取值范围是．

正确答案

解析

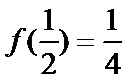
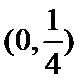
由题意可得函数的图像为下图，从图象上观察当关于X的方程为f(x)=m恰有三个互补相当的实数根时，函数的图形和直线y=m由三个不同的交点。再根据函数的极大值，可得m的取值范围为，所以填

考查方向

根的存在性及根的个数判断；新定义公式定理；函数的性质及应用

解题思路

根据函数的解析式画出函数的图像，然后确定实数的取值范围。

易错点

计算错误，考虑情况不完全

知识点

函数零点的判断和求解分段函数模型

1

题型：填空题

|

填空题 · 4 分

14．若函数（且）的值域是，则实数的取值范围是．

正确答案

解析

当，故，要使得函数的值域为，只需（）的值域包含于，故，所以，所以，解得，所以实数的取值范围是．

考查方向

分段函数求值域．

解题思路

分段函数是一个函数，其值域是各段函数值取值范围的并集，进而求出a的取值范围。

易错点

分段函数的分类讨论思想运用不好。

知识点

分段函数模型

1

题型：单选题

|

单选题 · 5 分

9．某车间分批生产某种产品，每批的生产准备费用为800元。若每批生产件，则平均仓储时间为，且每件产品每天的仓储费用为1元. 为使平均到每件产品的生产准备费用

与仓储费用之和最小，每批应生产产品（）

A60件

B80件

C100件

D120件

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

根据实际问题选择函数类型利用基本不等式求最值

1

题型：简答题

|

简答题 · 12 分

19．因发生意外交通事故，一辆货车上的某种液体泄露到一鱼塘中。为治理污染，根据环保部门的建议，现决定在鱼塘中投放一种可与污染液体发生化学反应的药剂。已知每投放个单位的药剂，它在水中释放的浓度y（克/升）随着时间（天）变化的函数关系式近似为，其中。若多次投放，则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和。根据经验，当水中药剂的浓度不低于4（克/升）时，它才能起到有效的治污的作用。

（1）若一次投放4个单位的药剂，则有效治污的时间可达几天？

（2）若因材料紧张，第一次只能投放2个单位的药剂，6天后再投放个单位的药剂，要使接下来的4天中能够持续有效治污，试求的最小值（精确到0．1，参考数据：取1．4）。

正确答案

解：（1）因为，所以，

①当时，由，解得，所以此时。

②当时，由，解得，所以此时。

综合得，，即，若一次投放4个单位的制剂，则有效治污时间可达8天。

（2）当时，，

由题意知，对于恒成立。

因为，而，所以，

故当且仅当时，有最小值为，

令，解得，所以的最小值为。

又，所以的最小值约为1．6。

解析

解析已在路上飞奔，马上就到！

知识点

分段函数模型函数模型的选择与应用利用基本不等式求最值

1

题型：填空题

|

填空题 · 5 分

9.经市场调查，某超市的一种小商品在过去的近20天内的日销售量（件）与价格（元）均为时间t(天)的函数，且日销售量近似满足g(t)=80-2t（件），价格近似满足f(t)=20-|t-10|（元），则该种商品在20天内的日销售额y的最大值为________.

正确答案

1225

解析

因为y=g(t)·f(t)=(80-2t)(20-|t-10|)=(40-t)(40-|t-10|)=

所以当0≤t≤10时，y的取值范围是[1200，1225]

在t=5时，y取得最大值为1225；

当10≤t≤20时，y的取值范围是[600，1200]，

在t=10时，y取得最大值为1200.

知识点

函数单调性的性质函数的最值二次函数的图象和性质分段函数模型

1

题型：单选题

|

单选题 · 5 分

7．设函数,则 ( )

A7

B9

C11

D13

正确答案

A

解析

因为

所以

所以所以选A

考查方向

分段函数的性质，求函数的值

解题思路

按照对数函数和指数函数的计算公式依次求解

易错点

计算错误

知识点

分段函数模型

1

题型：简答题

|

单选题

企业从业人员协调与上司之间的关系，其正确的做法是（）

A．如果认为上司委派自己的工作不合理，可以直接拒绝
B．对上司委派而自己干不了或干不好的工作，不能推辞
C．尊重上司的隐私，不在背地议论上司
D．对上司的错误指责，要敢于当面争辩以维护自身利益

正确答案

C

解析

暂无解析

1

题型：填空题

|

填空题 · 5 分

将一块半径为2 cm的半圆形铁皮卷成一个圆锥形（无底）容器，则它的容积为。

正确答案

解析

略

知识点

根据实际问题选择函数类型

1

题型：简答题

|

简答题 · 14 分

如图所示，有一块半径长为1米的半圆形钢板，现要从中截取一个内接等腰梯形部件，设。

（1）若用一种金属线条对梯形部件镶边，求最少需要准备该金属线条多少米；

（2）求梯形部件面积的最大值。

正确答案

见解析。

解析

如图所示，以直径所在的直线为轴，线段中垂线为轴，建立平面直角坐标系，设，过点作于，则，∴，

（1）∵，∴，

设的周长为，则.

下面只需要求的最大值.

令，则，

∴，即当时，有最大值5.

（2）

（方法1），令，则，令，，当时，，当时，，所以当时，有最大值，有最大值.

（方法2），令，∴，，.且当时，，当时，，

所以当时，有最大值.

（方法3）设（），过点作于，则，，

，

令，得，即，（舍），且当时，，当时，，所以当时，有最大值.

知识点

根据实际问题选择函数类型利用导数求函数的最值

1

题型：简答题

|

简答题 · 13 分

19．如图，已知中，．设，它的内接正方形DEFG的一边EF在斜边AB上，D、G分别在AC、BC上。假设的面积为S，正方形DEFG的面积为T 。

（1）用表示的面积S和正方形DEFG的面积T；

（2）设，试求的最大值P，并判断此时的形状；

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

根据实际问题选择函数类型解三角形的实际应用

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点