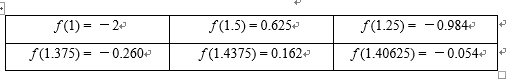- 函数模型及其综合应用
- 共61题
17.如图所示,













正确答案
选址应满足

解析
试题分析:本题属于解三角形应用题,题目的理解有一定难度,要注意读懂题意,选择函数模型来解决是本题的关键。
解法一:由条件①,得
设
则
所以点


所以当


即选址应满足

解法二:以



则
由条件①,得
设

化简得,
即点



则当



所以点

考查方向
解题思路
本题解三角形的应用题,解题步骤如下:
1、弄清题意,分清条件和结论,理顺数量关系。
2、建立相应数学模型。
3、利用正弦定理、余弦定理、求函数最值求解数学模型。
4、得出数学结论。
易错点
1、不能准确读懂题意,理顺数量关系。
2、转化为解三角形问题时,点

知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某商场2013年一月份到十二月份月销售额呈现先下降后上升的趋势,现有三种函数模型:
①



能较准确反映商场月销售额


正确答案
③,
解析
略
知识点
某市旅游部门开发一种旅游纪念品,每件产品的成本是





(1)写出

(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大。
正确答案
见解析。
解析
(1)改进工艺后,每件产品的销售价为


∴



(2)由


当



∴函数


故改进工艺后,产品的销售价为
知识点
若函数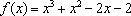
那么方程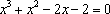
正确答案
解析
略
知识点
如图,建立平面直角坐标系




(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标
正确答案
(1)10千米;(2)当
解析
(1)在


由实际意义和题设条件知
∴

∴炮的最大射程是10千米。
(2)∵


即关于

由

此时,
∴当
知识点
噪声污染已经成为影响人们身体健康和生活质量的严重问题. 实践证明,声音强度





(1)当声音强度






(2)当人们低声说话,声音能量为






正确答案
(1)

解析
(1)



(2)由题意得


答:当声音能量
知识点
21。某旅游景点预计2013年1月份起前x个月的旅游人数的和p(x)(单位:万人)与x的关系近似地满足
(1)写出2013年第x月的旅游人数
(2)试问2013年第几月旅游消费总额最大,最大月旅游消费总额为多少元?
正确答案
见解析。
解析
(1)当

当


验证

(2)第
即
当



解得








当




综上,2013年第5月份的旅游消费总额最大,最大消费总额为3125万元. …12分
知识点
17.某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗





正确答案
解:设每天生产甲产品


由题意


可行域如图所示,
…………7分
把







解方程组



所以
答:每天生产甲产品

解析
解:设每天生产甲产品


由题意


可行域如图所示,
…………7分
把







解方程组



所以
答:每天生产甲产品

考查方向
简单线性规划问题(用平面区域表示二元一次不等式组) 等考点的理解
解题思路
线性规划问题求解步骤:
(1)确定目标函数;
(2)作可行域;
(3)作基准线(z=0时的直线);
(4)平移找最优解;
(5)求最值。
易错点
简单的线性规划中可行域的确定
教师点评
根据题设中的条件可设每天生产甲种产品x桶,乙种产品y桶,根据题设条件得出线性约束条件以及目标函数求出利润的最大值即可
知识点
17. 某油库的设计容量为30万吨,年初储量为10万吨,从年初起计划每月购进石油 




(1)试写出第


(2)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超过油库的容量,试确定
正确答案
见解析
解析
解:(1)
(2)根据题意
所以
即 
考查方向
解题思路
本题考查函数不等式的应用.解题步骤如下:
(1)求出函数表达式。
(2)根据函数值域,列出不等式。
(3)用换元法求出
易错点
不等式恒成立分析不够
知识点
扫码查看完整答案与解析