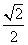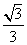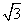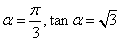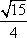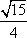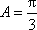- 三角函数的概念、同角三角函数的关系式和诱导公式
- 共714题
14.在平行四边形ABCD中,

正确答案
1
解析
设
如图
考查方向
解题思路
本题的解题思路
1)构造基底
2)使用三角形法则和平行四边形法则求出
3)根据数量积运算得出结果
易错点
本题易于错在数量积运算错误
知识点
若a∈(0, 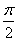
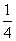
正确答案
解析
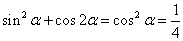
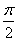
知识点
已知


正确答案
解析
略
知识点
设△ABC的内角A,B,C的对边分别为a,b,c,且a=1,b=2,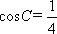
正确答案
解析
由余弦定理得c2=a2+b2-2abcosC=4,故c=2,而sinC=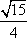
知识点
在△ABC中,角A,B,C所对的边分别为a,b,c. 已知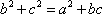
(1)求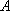
(2)如果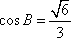
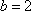

正确答案
(1)
(2)a=3
解析
(1)解:因为 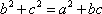
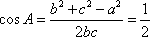
又因为 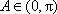
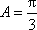
(2)解:因为 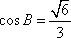
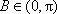
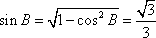
由正弦定理 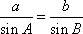
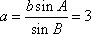
知识点
已知




则
正确答案
解析
略
知识点
正确答案
解析
知识点
正确答案
解析
知识点
已知


正确答案
解析
略
知识点
15.在





正确答案
解析
由

考查方向
本题考查解三角形和三角函数知识。
解题思路
由已知确定a,c的两个方程可解得。
易错点
求解方向不明,无法借助所学知识转化,或者运算出错。
教师点评
本题考查了正弦定理,余弦定理,平方关系等知识,在近几年的各省高考题出现的频率较高,常与三角恒等变换等知识点交汇命题。
知识点
扫码查看完整答案与解析