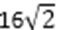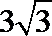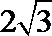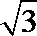- 与球体有关的内切、外接问题
- 共43题
三棱锥S-ABC的所有顶点都在球O的表面上，SA
A
B
C3
D12
正确答案
解析
略
知识点
已知点P，A，B，C，D是球O表面上的点，PA⊥平面ABCD，四边形ABCD是边长为
正确答案
解析
如图所示，∵PA⊥平面ABCD，
∴PA⊥AC。
故可知PC为球O直径，则PC的中点为O，取AC的中点为O′，
则
又∵
∴
∴球半径
∴△OAB为等边三角形。
∴
知识点
若一个球的表面积为
正确答案
1或7
解析
略
知识点
已知空间4个球，它们的半径均为2，每个球都与其他三个球外切，另有一个小球与这4个球都外切，则这个小球的半径为
A
B
C
D
正确答案
解析
由题意可知，小球球心
知识点
12．已知矩形ABCD的顶点都在半径为5的球O的球面上，且AB=8，
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．如图，在一个正方体内放入两个半径不相等的球
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．已知矩形ABCD的顶点都在半径为5的球O的球面上，且AB=8，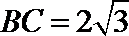
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．在三棱锥A—A′B′C′中，已知AA′⊥平面ABC，AA′=2，BC=
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．正四面体ABCD的棱长为4，E为棱BC的中点，过E作其外接球的截面，则截面面积的最小值为__________。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11.已知球的直径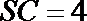
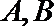
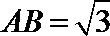
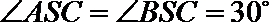
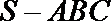
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析