- 与球体有关的内切、外接问题
- 共43题
9.三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直,且长度分别为3、4、5,则三棱锥P-ABC外接球的表面积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.一个正四棱柱的各个顶点在一个直径为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知四棱锥P-ABCD的五个顶点均在同一个球面上,该四棱锥的三视图如图,则在球内任取一点Q,则点Q在四棱锥P-ABCD内的概率为_________
正确答案
解析
由三视图可知,四棱锥P-ABCD放在长方体中如图所示,
外接球的半径为R=
所以外接球的体积V球=
故所求概率P=
知识点
16.已知四棱锥P-ABCD的五个顶点均在同一个球面上,该四棱锥的三视图如图,则在球内任取一点Q,则点Q在四棱锥P-ABCD内的概率为_________
正确答案
解析
由三视图可知,四棱锥P-ABCD放在长方体中如图所示,
外接球的半径为R=
所以外接球的体积V球=
故所求概率P=
知识点
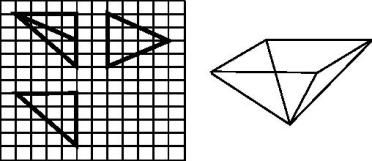
9.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,以该多面体的各条棱中最长的棱为标准截取8根等长的铁丝接成如图的四棱锥形骨架,把一个皮球放入该四棱锥形骨架内,使皮球的表面与8根铁丝都相切,则皮球的表面积为________
正确答案
36π
解析
解析已在路上飞奔,马上就到!
知识点
6.在边长为1的正方形ABCD内任取一点P,则动点P到点A和C的距离都小于1的概率是( )
正确答案
解析
满足条件的正方形ABCD如图所示,
其中满足条件的动点P的平面区域如图中阴影部分,
则正方形的面积S正方形=1,
阴影部分的面积S阴影=
故所求事件的概率为
知识点
10.点A,B,C,D在同一个球的球面上,AB = B


正确答案
解析
AB=BC=AC=√3∴四面体ABCD体积最大时,D在ABC的另一个半球内正△ABC面积=3√3/4∴高=4∴D到面ABC距离=4ABC所在面的圆心为O'球心为O∴O'A=O'B=O'C=2√3×√3×sin60°=1设球的半径为R勾股定理得(4-R)²+1²=R²解得R=17/8∴表面积=4πR²=289/16
考查方向
本题主要与球体有关的计算、四面体体积最值问题。属于较难题
解题思路
先找到四面体体积最大时球的半径,然后再求表面积
易错点
找不到四面体体积最大时的情况,忘记球表面积计算公式
知识点
15. 在四棱锥



正确答案
解析
根据已知条件,可求外接球的半径为
所以表面积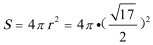
所以表面积为
考查方向
解题思路
先根据已知条件求外接球的半径,然后根据表面积公式求外接球的表面积
易错点
求外接球的半径
知识点
16.一个几何体由八个面围成,每个面都是正三角形,有四个顶点在同一平面内且为正
方形,若该八面体的棱长为2,所有顶点都在球O上,则球O的表面积为 .
正确答案
8π
解析
由题意知该八面体为两个等大的正四棱锥底面相对而成,由于八面体所以顶点都在同一个球面上,所以球O的球心在正四面体的底面中心处,此时O到所以顶点的距离均为

考查方向
解题思路
1.先明确题中给出的八面体的形状;
2.根据几何体的形状找到球心在正四棱锥底面中心处,进而求出球的半径,最后求出球的体积。
易错点
1.对于题中出现的八面体想象不出来是什么形状导致根本无从下手;
2.对于几何体外接球的球心的位置确定不了。
知识点
12. 四面体







正确答案
解析
如图,




考查方向
解题思路
因为AB
易错点
没有注意到垂直问题,以致于不能找出球的直径
知识点
扫码查看完整答案与解析