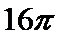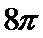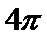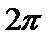- 与球体有关的内切、外接问题
- 共43题
1
题型:
单选题
|
体积为8的正方体的顶点都在同一球面上,则该球面的表面积为( )
正确答案
A
知识点
球的体积和表面积与球体有关的内切、外接问题
1
题型:
单选题
|
11.在半径为1的球面上有不共面的四个点A,B,C,D且



正确答案
C
解析
构造一个长方体,使得四面体ABCD的六条棱分别是长方体某个面的对角线(如图).设长方体的长、宽、高分别为


考查方向
空间几何体的计算。
解题思路
构造法来解。
易错点
缺乏空间想象力。
知识点
球面距离及相关计算与球体有关的内切、外接问题
1
题型:填空题
|
16. 




正确答案
32
解析
如下图所示:


考查方向
球的表面积问题。
解题思路
先求出球的半径再计算其表面积。
易错点
不会计算球的半径。
知识点
球面距离及相关计算球的体积和表面积与球体有关的内切、外接问题
1
题型:
单选题
|
8. 三棱锥P-ABC的三条侧棱两两垂直,三个侧面的面积分别是


正确答案
C
解析
因为三条侧棱两两垂直,所以可设



考查方向
球的体积和表面积;球内接多面体
解题思路
三棱锥的外接球实际上是它扩展为长方体的外接球,求长方体的对角线的长,就是球的直径,然后求球的体积
易错点
立体感不强;计算能力弱
知识点
棱柱、棱锥、棱台的体积与球体有关的内切、外接问题
1
题型:
单选题
|
11.正三棱锥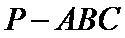
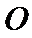
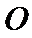
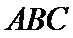
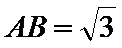
表面积为( )
正确答案
C
解析
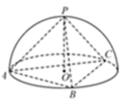
如下图所示,由题意得球心O为等边三角形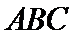
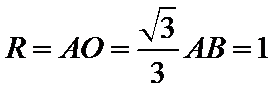
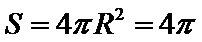
考查方向
本题主要考查了几何体的外接球、球的表面积计算等问题,在近几年的各省高考题出现的频率较高,常与几何体的表面积、体积等知识点交汇命题。
解题思路
先根据题意求出半径,再利用球的表面积公式求球的表面积。
易错点
不知如何建立模型求球的半径导致本题出错。
知识点
与球体有关的内切、外接问题
已完结
扫码查看完整答案与解析