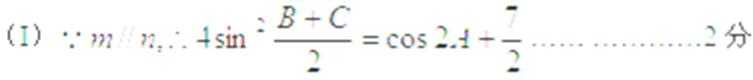- 三角函数中的恒等变换应用
- 共232题
18. 在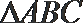
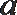
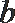
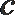
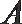
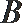

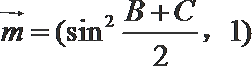
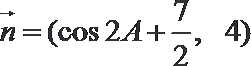
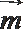
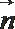
(Ⅰ) 求角
( II ) 当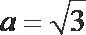
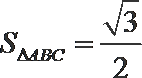
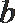
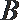
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7 .已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.如图,在平面直角坐标系













(Ⅰ)当直线


(Ⅱ)当


(Ⅲ)对任意

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知向量
(1)若

(2)记函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
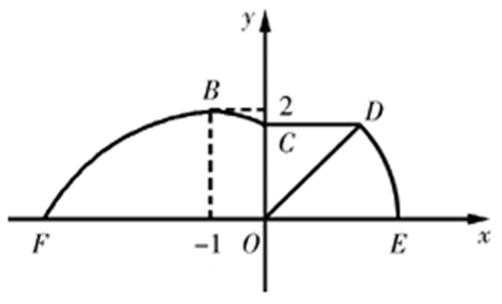
20.如图,某市准备在道路EF的一侧修建一条运动比赛道,赛道的前一部分为曲线段FBC.该曲线段是函数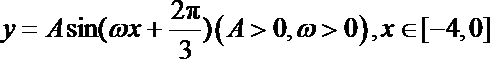


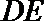
(Ⅰ)求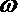
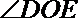
(Ⅱ)若要在圆弧赛道所对应的扇形ODE区域内建一个“矩形草坪”,矩形的一边在道路EF上,一个顶点在半径OD上,另外一个顶点P在圆弧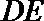
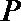
正确答案
(Ⅰ)由条件,得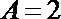
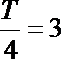
∵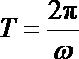
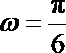
∴ 曲线段FBC的解析式为
当x=0时,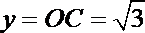
又CD=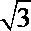
∴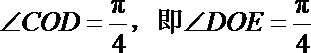
(Ⅱ)由(Ⅰ)知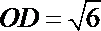
当“矩形草坪”的面积最大时,
点P 在弧DE上,故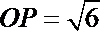
设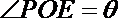
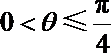
“矩形草坪”的面积为
=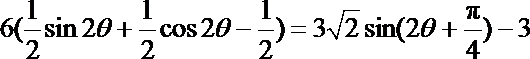
∵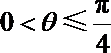
故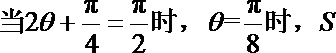
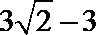
解析
解析已在路上飞奔,马上就到!
知识点
18. 节能灯的质量通过其正常使用时间衡量.使用时间越长,表明质量越好,若使用时间小于4千小时的产品为不合格品;使用时间在4千小时到6千小时的产品为合格品;使用时间大于6千小时的产品为优质品.某节能灯生产厂家为了解同一型号的某批次产品的质量情况,随机抽取了部分产品作为样本.得到试验结果的频率分布直方图如图所示.若以上述试验结果中使用时间落人各组的频率作为相应的概率.
(I)若该批次有产品2000件,试估计该批次的不合格品,合格品,优质品分别有多少件?
(II)已知该节能灯生产厂家对使用时间小于6千小时的





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.关于函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求函数
(2)在给出的平面直角坐标系中,画出函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析